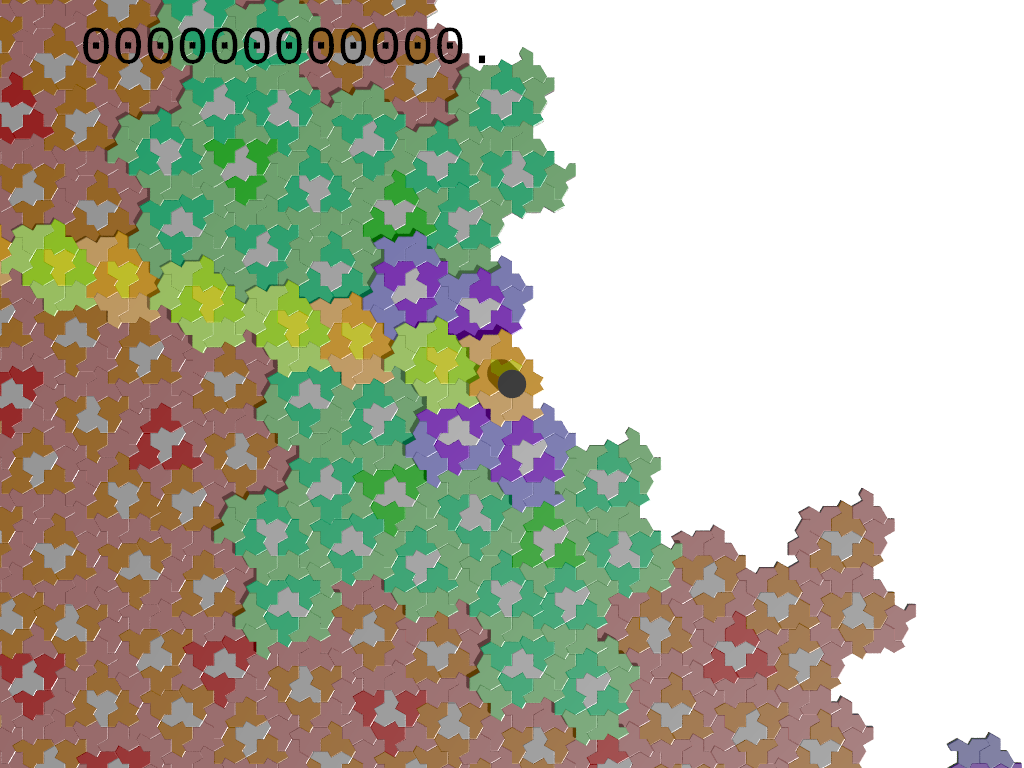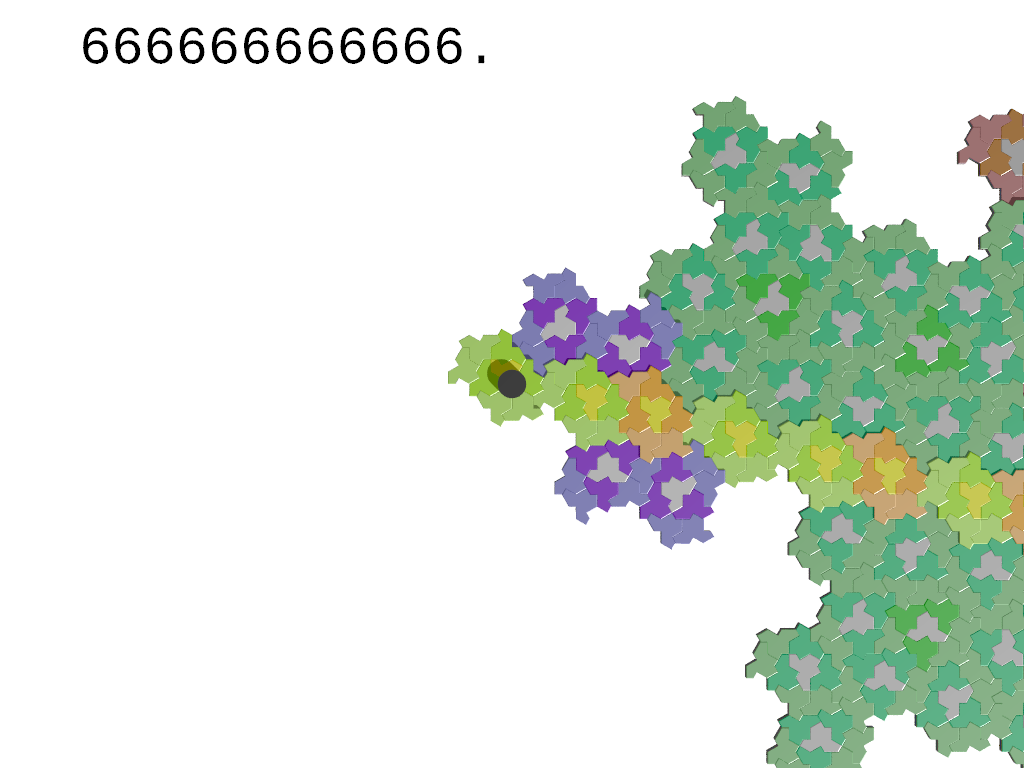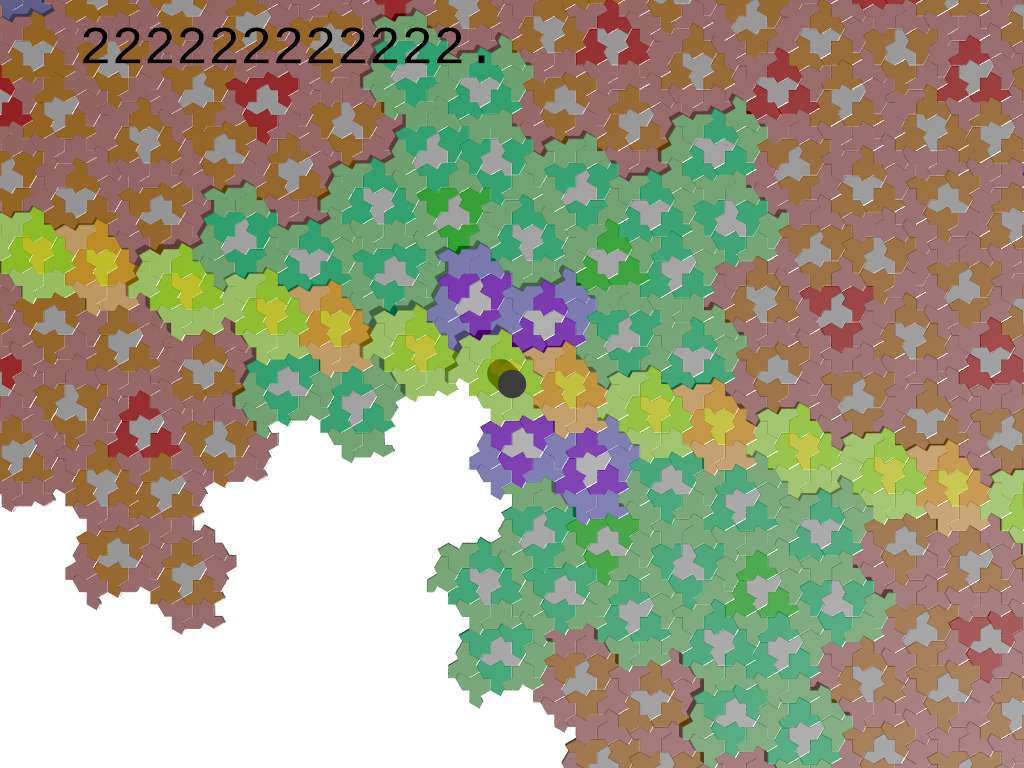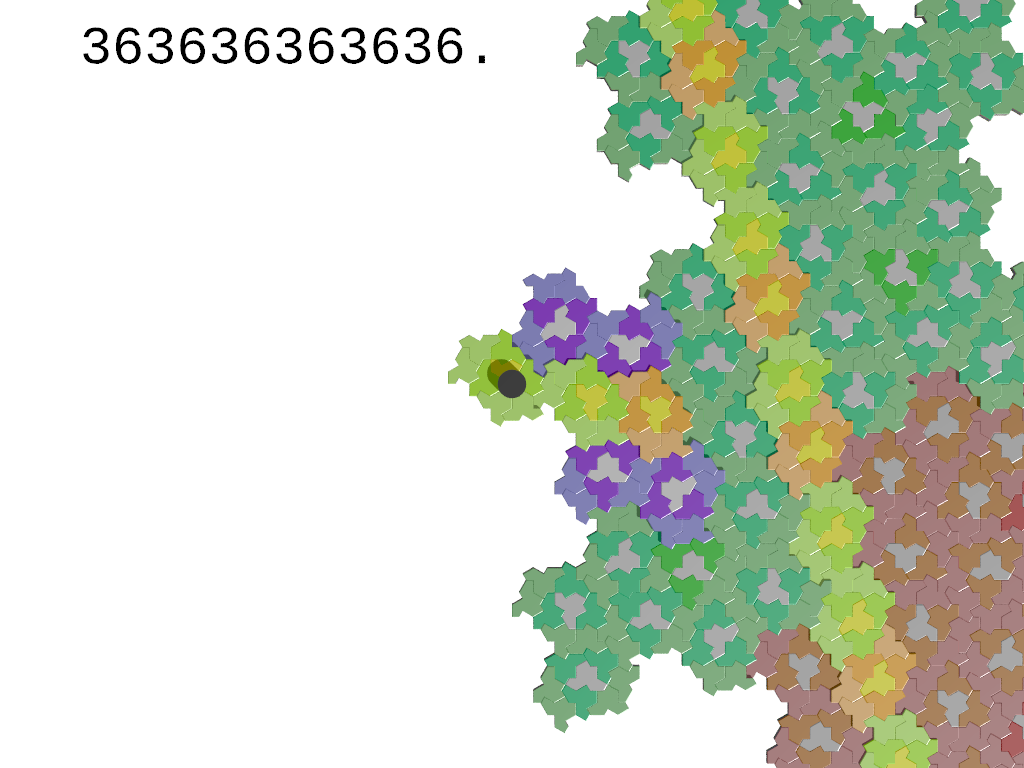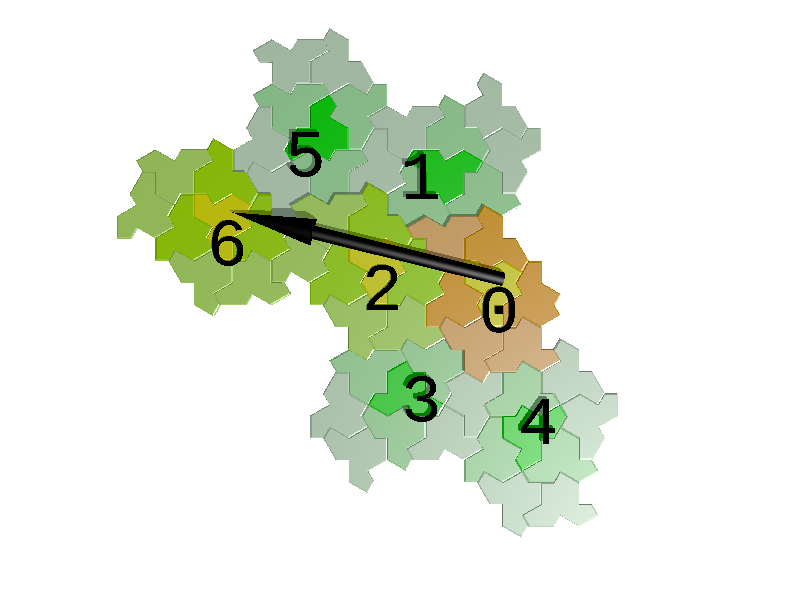
The meaning of the symbols is clarified in the image on the left showing the subdivision process for a tile "8".
In a signature we do not allow for the consecutive pair of symbols ...06...
The notation "[w]p." denotes the periodic signature "...wwwwp." where w is any nonempty finite sequence of symbols and p is a possibly empty finite sequence of symbols.
A tile is part of an infinite worm if and only if its signature contains only symbols in {0,2,6};
An infinite worm is described as a bi-infinite sequence of tiles "8" and "7" conventionally oriented as illustrated.