Fractal limits of the H7 and H8 clusters

By repeating the subdivision process for clusters H7 and H8 (see here) and suitably rescaling the resulting superclusters we get in the limit two fractal shapes:
H8 H7
In order to compute (at least heuristically) the Hausdorff dimension of the fractal boundary we need to devise an appropriate subdivision process for the boundary alone.

This can be done by partitioning the boundary (of e.g. the fractal H8) in four pieces A, B, C, D and showing how to obtain these four pieces as (an essentially disjoint) union of smaller copies of themselves. This is illustrated in this image:

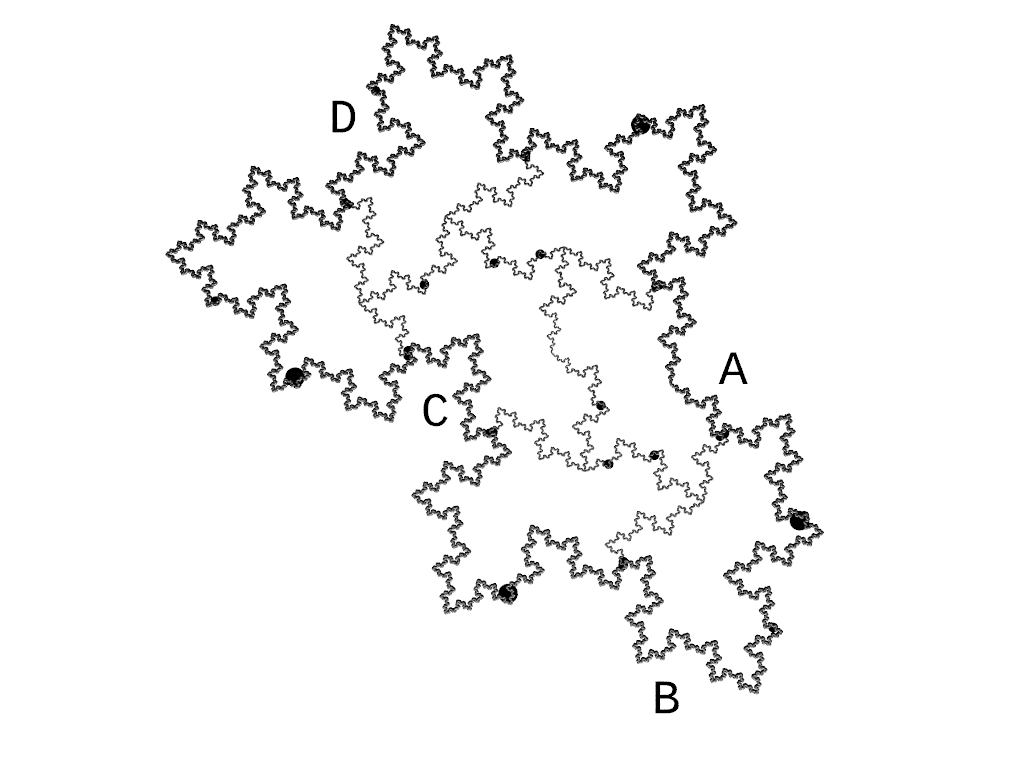
We end up with the substitution system
A -> dab
B -> cdc
C -> dcb
D -> cdcdc
where the small letters refer to the smaller copies. We seek the dimension \( \delta \) for which the corresponding Hausdorff measures are positive and finite real numbers. By enforcing \( |A| = \gamma |a|, |B| = \gamma |b| \) etc for some \( \gamma \gt 1 \), after a short computation we obtain \( \gamma = 2 + \sqrt{3} \) and the corresponding Hausdorff measures of the four pieces satisfying \( |a| = |b| = |c|; |d| = \sqrt{3}|a| \).
The resulting (formally computed) Hausdorff dimension of the fractal boundary is then given by \[ d = \frac{\log (2+\sqrt{3})}{\log (\frac{3+\sqrt{5}}{2})} \approx 1.368376490708324 \] Obtained by enforcing the fact that the linear growth factor is \( \Phi^2 = (3+\sqrt{5})/2 \).