Worms in spectre tilings

Hydra: a pair of remarkable almost C-6 rotationally symmetric tilings (hydra and hydra2) discovered by Pieter Mostert with 4 half-infinite, one bi-infinite worms and 4 half-infinite plus one bi-infinite wriggly worms. By reverting the bi-infinite worms one can obtain 12 distinct configurations in two equivalent classes if we allow for 60 degrees rotations.
The tripod pair (by Joshua Socolar) has the interesting feature of having two possible bi-infinite worms sharing the first half of their path.
Short animation showing how the worm is reverted

Back

less-wriggly worms

Worms (or snakes) are wiggling sequences of tiles that can be all reverted without any perturbation of the surrounding tiles except at the worm tip and tail. As a consequence, a bi-infinite worm can be reverted without influence on the rest of the tiling. The black worm in the images connects the boundary point with address "...333." to the base point with address "[0].". Observe that only at odd depths this worm walks through the center (address "[40]." or "[04]." where the tripod observed by Joshua Socolar is located.
The green paths show potential worms. Most of them have an internal tip (end point), thus cannot be bi-infinite.

depth 4	depth 5	depth 6

Wriggly worms

In addition to the worms shown above we can find wriggly worms, shown in white here.

depth 5	Zoom	Alternate black worm

depth 6	Zoom

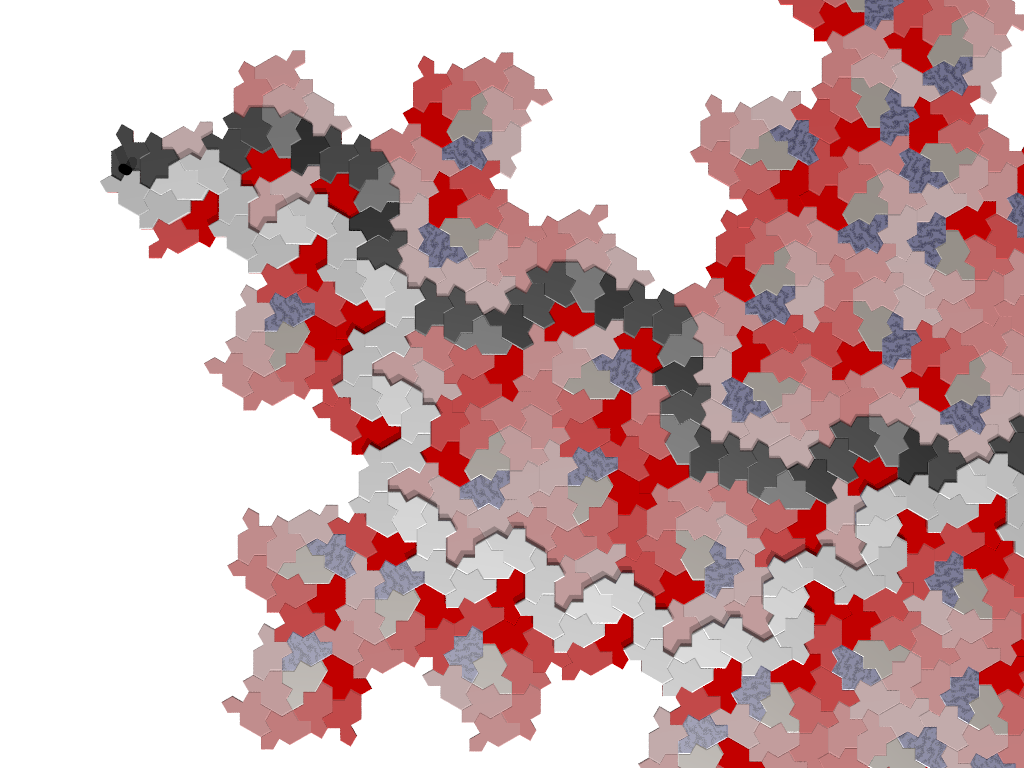
A zoom of one of the images above

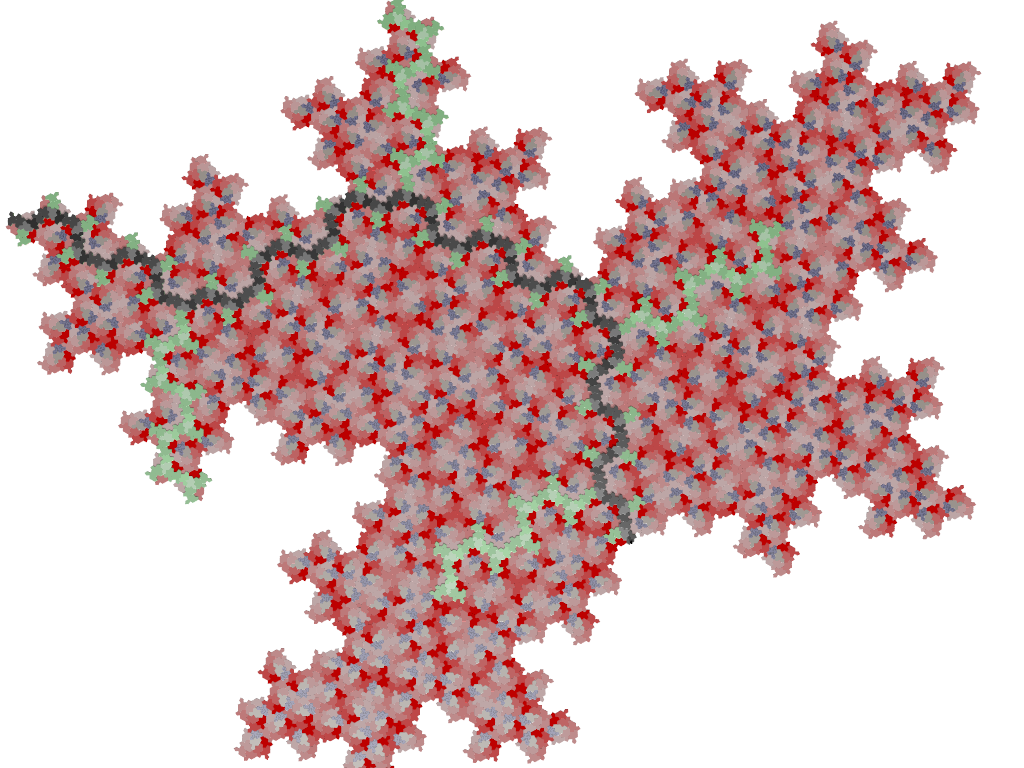
The two hydra tilings

[See also here to find the same two tilings from the perspective of their Conway signature] Partial tiling with Conway signature "[5]." has density 5/6 (roughly meaning that it covers 5/6 of the plane) and can be completed into a full tiling by disjoint union with the partial tiling "[3].". Looking at it from the point of view of worms and wriggly worms we find one bi-infinite worm and one bi-infinite wriggly worm, both passing through the central point. In addition we find four semi-infinite worms and four semi-infinite wriggly worms. Upon removal of all these infinite and semi-infinite worms we are left with a 60 degrees rotationally symmetric structure.

Tiling core	Overview	Zoom
Hydra 1

Hydra 2

The two tilings above after reversal of the black worm:

Hydra 1 with black worm reverted	Hydra 2 with black worm reverted

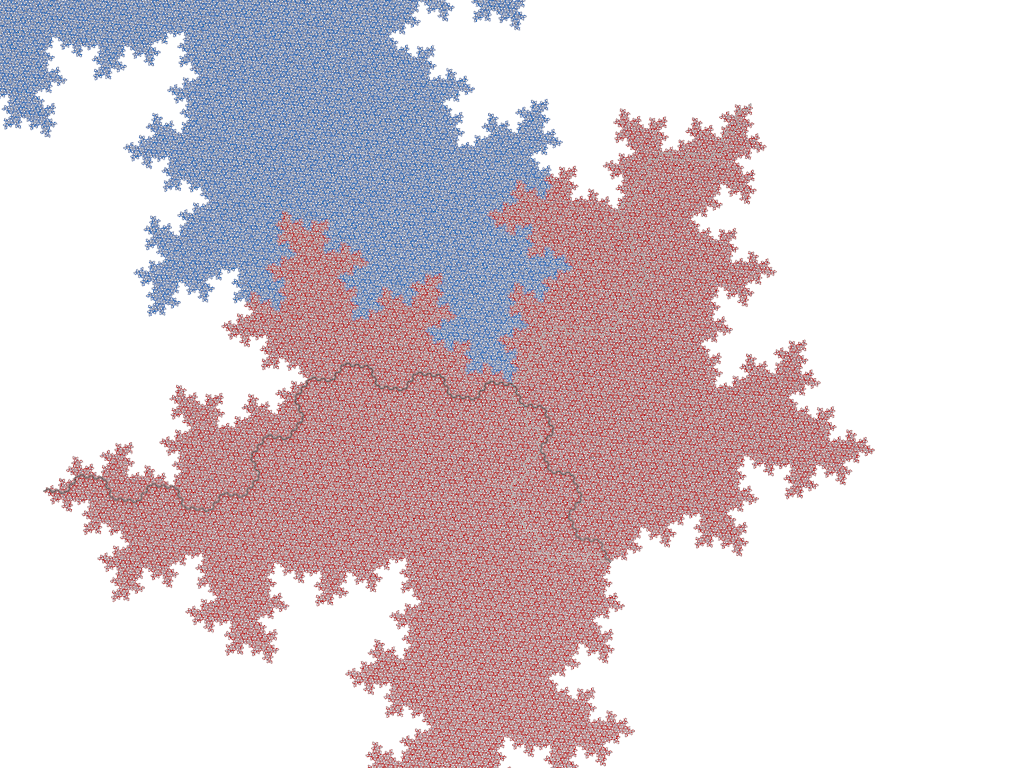
The tripod tilings

They are actually two tilings that alternate by subdivision having signature respectively "[40]." and "[04].". The interesting feature is the presence of two complete worms sharing the first half (arriving from the South) and departing in two different directions.
Here the two tilings are computed respectively with depths 5 and 6.

Tiling core	Overview	Zoom