È il luogo dei punti (x,y) del piano che godono
della seguente proprietà: la
successione di punti definita per ricorsione da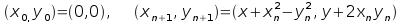 è una successione limitata.
Per chi ha dimestichezza con il piano dei numeri complessi, tale
successione si scrive
è una successione limitata.
Per chi ha dimestichezza con il piano dei numeri complessi, tale
successione si scrive
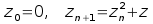 ,
dove
,
dove
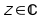 .
Nella formula appena scritta, operare per ricorsione significa che il
passo successivo viene calcolato a partire dai passi precedenti (un
po' come nei numeri di Fibonacci, insomma). Per esempio: per capire
se il punto (2,1) appartiene o no all'insieme di Mandelbrot dobbiamo
costruire la successione
.
Nella formula appena scritta, operare per ricorsione significa che il
passo successivo viene calcolato a partire dai passi precedenti (un
po' come nei numeri di Fibonacci, insomma). Per esempio: per capire
se il punto (2,1) appartiene o no all'insieme di Mandelbrot dobbiamo
costruire la successione
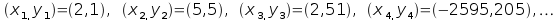 che
è evidentemente illimitata (anche se andrebbe dimostrato), quindi il
punto (2,1) non appartiene all'insieme di Mandelbrot. Se invece
consideriamo banalmente il punto (-1,0) abbiamo
che
è evidentemente illimitata (anche se andrebbe dimostrato), quindi il
punto (2,1) non appartiene all'insieme di Mandelbrot. Se invece
consideriamo banalmente il punto (-1,0) abbiamo
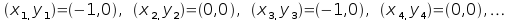 e
la successione continua a oscillare tra i valori (-1,0) e (0,0),
quindi in particolare è limitata. Il punto (-1,0) dunque appartiene
all'insieme di Mandelbrot. Ovviamente i conti non sono sempre così
facili: ad esempio, da una piccola simulazione al calcolatore risulta
che la successione costruita a partire dal punto
(-1.1635189,0.22928247) è limitata e converge verso una successione
periodica di periodo 72 (sì, settantadue). Chiaramente, accorgersi
che una successione ha questo periodo richiederebbe una notevole
quantità di conti, se provata “a mano”. Per fortuna la
matematica ci può aiutare ad effettuare almeno alcue stime iniziali.
Per cominciare: i punti fuori dal cerchio di centro l'origine e
raggio 2 non appartengono all'insieme di Mandelbrot; questo intanto
garantisce che l'insieme è limitato. Inoltre vale un “criterio di
uscita”: senza dover scomodare l'infinito, se capita che la
successione dei punti ad un certo passo esca dal cerchio di centro
l'origine e raggio 2, allora è illimitata, e il punto di partenza è
da scartare. Come si può capire, tale criterio torna molto utile in
una costruzione al calcolatore dell'insieme di Mandelbrot. Una
rappresentazione approssimata dell'insieme di Mandelbrot è la
seguente, fornita dal programma Xaos:
e
la successione continua a oscillare tra i valori (-1,0) e (0,0),
quindi in particolare è limitata. Il punto (-1,0) dunque appartiene
all'insieme di Mandelbrot. Ovviamente i conti non sono sempre così
facili: ad esempio, da una piccola simulazione al calcolatore risulta
che la successione costruita a partire dal punto
(-1.1635189,0.22928247) è limitata e converge verso una successione
periodica di periodo 72 (sì, settantadue). Chiaramente, accorgersi
che una successione ha questo periodo richiederebbe una notevole
quantità di conti, se provata “a mano”. Per fortuna la
matematica ci può aiutare ad effettuare almeno alcue stime iniziali.
Per cominciare: i punti fuori dal cerchio di centro l'origine e
raggio 2 non appartengono all'insieme di Mandelbrot; questo intanto
garantisce che l'insieme è limitato. Inoltre vale un “criterio di
uscita”: senza dover scomodare l'infinito, se capita che la
successione dei punti ad un certo passo esca dal cerchio di centro
l'origine e raggio 2, allora è illimitata, e il punto di partenza è
da scartare. Come si può capire, tale criterio torna molto utile in
una costruzione al calcolatore dell'insieme di Mandelbrot. Una
rappresentazione approssimata dell'insieme di Mandelbrot è la
seguente, fornita dal programma Xaos:

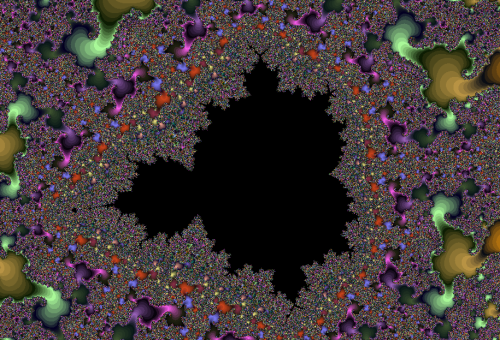
I
punti che appartengono all'insieme di Mandelbrot sono quelli colorati
di nero. I colori della parte esterna dipendono dal numero di passi
che la successione ha impiegato per uscire dal cerchio di centro
l'origine e raggio 2, e quindi per essere certi che fosse illimitata.
Per
indagare le proprietà dell'insieme di Mandelbrot sono necessari
strumenti matematici piuttosto sofisticati; alcune sue proprietà
sono tuttora oggetto di ricerca. Ad esempio, è stato dimostrato solo
pochi anni fa (1994) dal matematico giapponese Mitsuhiro Shishikura
che il bordo dell'insieme di Mandelbrot ha dimensione di Hausdorff 2
(quindi è una curva piuttosto “spessa”, per quanto abbiamo visto
prima). Non è ancora chiaro, invece, se l'insieme di Mandelbrot sia
connesso, ovvero se presi due punti qualsiasi dell'insieme di
Mandelbrot esista una curva continua, tutta contenuta nell'insieme,
che li congiunge. L'insieme di Mandelbrot è incredibilmente ricco di
dettagli: al suo interno si possono ritrovare delle copie “quasi”
uguali di se stesso, quindi in un certo senso presenta le
caratteristiche dell'autosimilarità, come si vede in questa figura
(ottenuta ingrandendo circa 5000 volte una certa zona dell'insieme di
partenza).
Esistono
però altre zone in cui l'insieme si ramifica in modo molto sottile,
e questi rami a loro volta si ramificano, dando luogo a quella che,
ormai anche simbolicamente, è definita come la struttura frattale.
Ne vediamo un esempio nella figura seguente, che rappresenta un altro
particolare fortemente ingrandito dell'insieme di Mandelbrot.

Passiamo
ora ad analizzare l'ultimo esempio tra quelli citati, ovvero
l'attrattore di Lorenz. Esso è legato al sistema di Lorenz, un
sistema di equazioni differenziali che rappresenta il prototipo del
“caos deterministico” o dell'effetto “farfalla”. Vale la pena
di raccontare brevemente la storia dell'attrattore di Lorenz e di
spiegare in dettaglio i termini citati sopra. Prima però devo
accennare brevemente al concetto di equazione differenziale:
un'equazione differenziale mette in relazione in qualche modo una
funzione e la sua derivata: risolvere l'equazione significa trovare
una funzione (e non semplicemente un numero) che soddisfa tale
relazione. Esempio semplice: ci si può chiedere quale funzione
soddisfi la proprietà di avere la derivata uguale al doppio di sé
stessa; in termini matematici bisogna risolvere l'equazione
differenziale f'(x)=2f(x), dove l'incognita è la funzione f(x) e
l'apice denota la derivata. In questo caso si può verificare che la
funzione
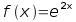 è
una soluzione di questa equazione.
Comunque, per capire quanto segue, non c'è bisogno per forza di
saper risolvere un'equazione differenziale, ma bisogna aver chiaro
che cosa significa che una funzione risolve l'equazione. Ovviamente,
la soluzione di un sistema
di equazioni differenziali è costituita da un gruppo di funzioni che
soddisfano contemporaneamente
tutte le equazioni differenziali del sistema.
è
una soluzione di questa equazione.
Comunque, per capire quanto segue, non c'è bisogno per forza di
saper risolvere un'equazione differenziale, ma bisogna aver chiaro
che cosa significa che una funzione risolve l'equazione. Ovviamente,
la soluzione di un sistema
di equazioni differenziali è costituita da un gruppo di funzioni che
soddisfano contemporaneamente
tutte le equazioni differenziali del sistema.
Il
sistema di Lorenz è il seguente sistema di tre equazioni
differenziali ordinarie del primo ordine non lineari:
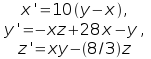 ,
dove si intende che x,y,z sono delle funzioni reali del tempo t e
x',y',z' le loro derivate prime. Tale sistema è stato introdotto
nello studio del movimento di masse d'aria calda all'interno
dell'atmosfera. Edward Lorenz, matematico e meteorologo statunitense,
negli anni sessanta per poter affrontare un certo problema legato
alle previsioni meteorologiche attuò una serie di semplificazioni,
anche piuttosto drastiche, e si ricondusse allo studio di queste tre
equazioni differenziali. Nonostante la notevole riduzione della
difficoltà del problema, il sistema di Lorenz risultò
particolarmente ostico da affrontare, ed anche le simulazioni
numeriche, che a quell'epoca cominciavano a diventare piuttosto
potenti, mostrarono un comportamento sorprendente.
,
dove si intende che x,y,z sono delle funzioni reali del tempo t e
x',y',z' le loro derivate prime. Tale sistema è stato introdotto
nello studio del movimento di masse d'aria calda all'interno
dell'atmosfera. Edward Lorenz, matematico e meteorologo statunitense,
negli anni sessanta per poter affrontare un certo problema legato
alle previsioni meteorologiche attuò una serie di semplificazioni,
anche piuttosto drastiche, e si ricondusse allo studio di queste tre
equazioni differenziali. Nonostante la notevole riduzione della
difficoltà del problema, il sistema di Lorenz risultò
particolarmente ostico da affrontare, ed anche le simulazioni
numeriche, che a quell'epoca cominciavano a diventare piuttosto
potenti, mostrarono un comportamento sorprendente.
Per
cominciare, è meglio “allontanare” la fisica dal nostro problema
e considerare il sistema di Lorenz dal punto di vista puramente
matematico. Quindi possiamo dimenticare il significato originario
delle funzioni x,y,z (significato che è legato all'evolversi nel
tempo di quantità come la temperatura e la densità dell'aria) e
pensare che siano le coordinate di un punto nello spazio. La
soluzione del sistema può essere quindi visualizzata, almeno in
linea di principio, come una curva nello spazio percorsa da un punto,
ovvero una traiettoria. Inoltre, per semplificare
ulteriormente il problema, ci si accontenta di trovarne non la
soluzione esplicita, bensì il comportamento per tempi lunghi
(comportamento asintotico). Questo vuol dire studiare l'attrattore
del sistema: cercare che cosa diventa la traiettoria del punto quando
il tempo trascorso diventa sempre più lungo. L'idea di base è che
il comportamento della traiettoria in tempi brevi è molto
influenzato da fenomeni esterni al sistema, come il punto di
partenza, mentre ciò che è veramente intrinseco al sistema è
quello che succede per tempi lunghi.
Le
maggiori difficoltà sono legate al coefficiente r=28 che moltiplica
la funzione x nella seconda equazione: infatti, per altri valori di
questo coefficiente (valori più piccoli, diciamo compresi tra 1 e
20) è evidente, anche mediante una simulazione numerica, che le
traiettorie del sistema vanno a schiacciarsi verso un punto
particolare, indipendentemente dalla posizione di partenza;
per valori più alti di r, al contrario, la traiettoria sembra
“vagare” nello spazio senza una meta apparente. Soprattutto, per
valori di r vicino a 28 è sufficiente variare di pochissimo la
posizione di partenza del punto per avere delle traiettorie alquanto
diverse, sebbene si trovino tutte in una zona ben precisa dello
spazio. Questo significa che due punti che si trovano molto vicini in
partenza e si muovono seguendo la legge del sistema di Lorenz, dopo
un po' di tempo potrebbero trovarsi molto lontani, per poi magari
“sfiorarsi” di nuovo dopo un po' e riallontanarsi ancora.
Riprendendo il significato fisico del sistema, di cui prima ci
eravamo volutamente liberati, da condizioni meteorologiche simili
(temperature, densità dell'aria, velocità del vento simili) possono
evolvere, seguendo il sistema di Lorenz, situazioni molto differenti
nel giro di poco tempo. Si parla in questo caso di dipendenza
sensibile dalle condizioni iniziali, o anche di caos
deterministico. È a questo tipo
di situazioni che ci si riferisce quando si parla di
effetto-farfalla: è sufficiente il battito d'ali di una farfalla per
modificare le condizioni atmosferiche iniziali e dunque provocare un
uragano a migliaia di chilometri di distanza (o, perché no, per
annullarne uno che altrimenti si sarebbe formato).
Ma
che cosa c'entrano i frattali con tutto questo discorso? Cerchiamo di
capire più in dettaglio come è fatta la traiettoria di un punto
quando si sceglie proprio 28 (o un numero più grande)
come valore per il parametro r. Provando a fare delle simulazioni al
calcolatore risulta che, indipendentemente dalla posizione iniziale,
le traiettorie hanno un andamento simile a quello mostrato in questo
disegno:
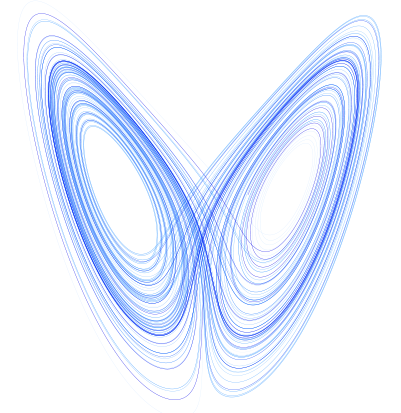
Si
noti come tale disegno può ricordare una farfalla! Si deve pensare
che questo disegno rappresenta una traiettoria tridimensionale,
quindi va pensato come visto in prospettiva. Seguendo con pazienza,
per quanto possibile, l'evolversi della traiettoria si vede che il
punto “si avvolge” per un po' di tempo attorno a uno dei due
centri, per poi spostarsi improvvisamente ed avvolgersi attorno
all'altro, quindi ritornare indietro per un po' e così via. Tale
traiettoria non si interseca mai con se stessa (questo violerebbe il
teorema di unicità della soluzione fissate le condizioni iniziali).
Il disegno precedente rappresenta quindi l'attrattore del sistema di
Lorenz, poiché tutte le traiettorie si avvicinano indefinitamente a
questo insieme, a patto di lasciare scorrere un tempo sufficiente.
L'attrattore di Lorenz è un frattale: in realtà è molto più
“pieno” di quanto il disegno non lasci trasparire; la sua
dimensione di Hausdorff è stimata essere di poco superiore a 2 (per
la precisione 2,06), quindi appena superiore a quella di una
superficie usuale. Quando un sistema ammette un attrattore che ha una
dimensione frazionaria, si parla di attrattore strano. Il
fatto che un sistema di equazioni differenziali presenti il fenomeno
del caos deterministico, ovvero che punti di partenza arbitrariamente
vicini evolvano verso posizioni molto distanti, va a braccetto col
fatto che ammetta un attrattore strano; i due fenomeni sono
strettamente legati. Di nuovo, vediamo che da una struttura
apparentemente semplice scaturisce un frattale e, come sempre quando
si è in presenza di queste figure, le cose sono sempre più
complicate di quello che sembravano a prima vista.
Insomma, per dirla con un acrostico, i Frattali Resistono A Tante
Teorie, A Lampi Ingegnosi; anche in questo sta il loro fascino
misterioso ed ammaliante. La matematica però è uno strumento
potentissimo che ci permette non solo di conoscere l'esistenza di
queste figure, ma anche di indagarle a fondo e svelarne la bellezza.



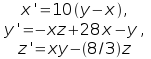 ,
dove si intende che x,y,z sono delle funzioni reali del tempo t e
x',y',z' le loro derivate prime. Tale sistema è stato introdotto
nello studio del movimento di masse d'aria calda all'interno
dell'atmosfera. Edward Lorenz, matematico e meteorologo statunitense,
negli anni sessanta per poter affrontare un certo problema legato
alle previsioni meteorologiche attuò una serie di semplificazioni,
anche piuttosto drastiche, e si ricondusse allo studio di queste tre
equazioni differenziali. Nonostante la notevole riduzione della
difficoltà del problema, il sistema di Lorenz risultò
particolarmente ostico da affrontare, ed anche le simulazioni
numeriche, che a quell'epoca cominciavano a diventare piuttosto
potenti, mostrarono un comportamento sorprendente.
,
dove si intende che x,y,z sono delle funzioni reali del tempo t e
x',y',z' le loro derivate prime. Tale sistema è stato introdotto
nello studio del movimento di masse d'aria calda all'interno
dell'atmosfera. Edward Lorenz, matematico e meteorologo statunitense,
negli anni sessanta per poter affrontare un certo problema legato
alle previsioni meteorologiche attuò una serie di semplificazioni,
anche piuttosto drastiche, e si ricondusse allo studio di queste tre
equazioni differenziali. Nonostante la notevole riduzione della
difficoltà del problema, il sistema di Lorenz risultò
particolarmente ostico da affrontare, ed anche le simulazioni
numeriche, che a quell'epoca cominciavano a diventare piuttosto
potenti, mostrarono un comportamento sorprendente.
