Finite element mesh generation
:
a Web page maintained by
Robert Schneiders at Lehrstuhl für angewandte Mathematik
insbesondere Informatik.
Motion by mean curvature.
 Click on the icon to view a detailed picture of a torus in the 4D space
(a slice of it, actually) flowing by mean curvature.
This picture is obtained with the
POVRAY package.
See also a few variants with different
textures.
Click on the icon to view a detailed picture of a torus in the 4D space
(a slice of it, actually) flowing by mean curvature.
This picture is obtained with the
POVRAY package.
See also a few variants with different
textures.
Crystalline motion by mean curvature.
We model motion by mean curvature in the particular case of a
poligonal Wulff shape (crystalline anisotropy) by means of an
Allen-Cahn type regularization, see
[GoPa96A].
Simulations include the presence of an $x$ dependent forcing term.
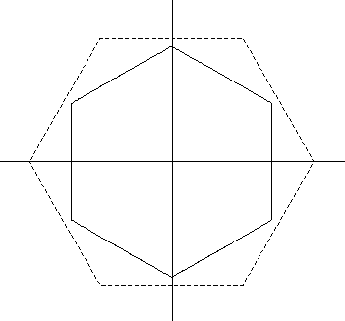 In this picture the solid line represents the Frank diagram of the
anisotropy, and the dashed line represents the corresponding
Wulff shape.
In this picture the solid line represents the Frank diagram of the
anisotropy, and the dashed line represents the corresponding
Wulff shape.
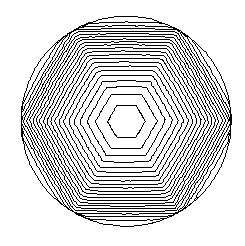 This is the corresponding evolution starting from a circle (no
forcing term).
This is the corresponding evolution starting from a circle (no
forcing term).
 Here the anisotropy is nonconvex, and the convexified gives an
hexagon. The "ears" in the Wulff shape correspond to the concave
parts in the Frank diagram.
Here the anisotropy is nonconvex, and the convexified gives an
hexagon. The "ears" in the Wulff shape correspond to the concave
parts in the Frank diagram.
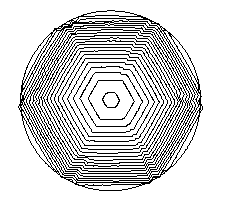 Starting from a circle, our Allen-Cahn approach without
convexification, gives the following result.
Note the formation of wrinklings of the size of the spatial discretization.
Starting from a circle, our Allen-Cahn approach without
convexification, gives the following result.
Note the formation of wrinklings of the size of the spatial discretization.
More simulations to be inserted here...
see pictures here.
Nonconvex motion by mean curvature, Perona-Malik equation.
Text to be inserted here.....

 MP,
Dec 6, 11
MP,
Dec 6, 11

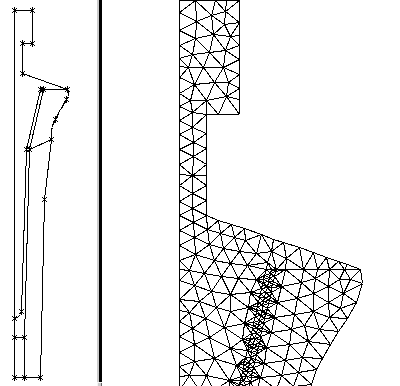 An example of typical domain divided into subdomains and
a zoom of the resulting
mesh after flipdiag and pigra
regularization.
The file
An example of typical domain divided into subdomains and
a zoom of the resulting
mesh after flipdiag and pigra
regularization.
The file
 Here is another example...
Here is another example...
 In this picture the solid line represents the Frank diagram of the
anisotropy, and the dashed line represents the corresponding
Wulff shape.
In this picture the solid line represents the Frank diagram of the
anisotropy, and the dashed line represents the corresponding
Wulff shape.
 This is the corresponding evolution starting from a circle (no
forcing term).
This is the corresponding evolution starting from a circle (no
forcing term).
 Here the anisotropy is nonconvex, and the convexified gives an
hexagon. The "ears" in the Wulff shape correspond to the concave
parts in the Frank diagram.
Here the anisotropy is nonconvex, and the convexified gives an
hexagon. The "ears" in the Wulff shape correspond to the concave
parts in the Frank diagram.
 Starting from a circle, our Allen-Cahn approach without
convexification, gives the following result.
Note the formation of wrinklings of the size of the spatial discretization.
Starting from a circle, our Allen-Cahn approach without
convexification, gives the following result.
Note the formation of wrinklings of the size of the spatial discretization.

