20
PROGRAMMI DEI CORSI
21
22
1. Algebra: prof.
MARIA CLARA TAMBURINI
A) PROGRAMMA DEL CORSO
1. Insiemi
Generalità. Relazioni binarie, applicazioni. Prodotto di applicazioni. Relazioni d'ordine. Relazioni di equivalenza e partizioni. Insieme quoziente. Equipotenza fra insiemi, cardinalità. Teorema di Cantor.
2. I numeri interi
Buon Ordinamento e principio di induzione. L'algoritmo della divisione. Massimo comune divisore e algoritmo delle divisioni successive. Relazioni di congruenza modulo n. Congruenze lineari. Equazioni diofantee. Teorema fondamentale dell'aritmetica. Numeri in base n.
3 Monoidi e gruppi
Generalità ed esempi. Gruppo simmetrico e gruppo alterno. Sottogruppo generato da un sottoinsieme, gruppi ciclici. Periodo di un elemento. Laterali di un sottogruppo. Teorema di Lagrange. Omomorfismi. Sottogruppi normali e gruppi quoziente. Teorema di Cayley. Prodotto diretto di gruppi.
4. Anelli e campi
Generalità ed esempi. Ideali e anelli quoziente. Omomorfismi. Caratteristica di un anello. Sottocampo minimo di un corpo. Campo dei quozienti di un dominio di integrità. Anelli di polinomi. Radici. Teorema di Ruffini.
5. Dominii fattoriali
Divisibilità in un dominio di integrità. Dominii euclidei e dominii a ideali principali. Teorema Cinese del resto. Anelli a fattorizzazione unica. Criteri per l'irriducibilità di un polinomio in R(x) e in Q(x). Lemma di Gauss, criterio di Eisenstein.
6. Matrici
Somma e prodotto di matrici. Determinanti. Operazioni elementari su righe e colonne. Forma normale di una matrice, fattori invarianti.
7. Moduli
Spazi vettoriali e moduli su un anello. Sottomoduli, omomorfismi e moduli quoziente. Torsione. Moduli ciclici, decomposizione primaria. Somme e prodotti diretti. Moduli liberi, basi. Teorema di struttura dei moduli finitamente generati su un dominio a ideali principali. Applicazioni agli spazi vettoriali e ai gruppi abeliani finitamente generati.
8. Forme canoniche delle matrici
La forma canonica razionale e la forma canonica di Jordan. Autovalori, autovettori.
9. Reticoli e algebre di Boole
I reticoli come insiemi parzialmente ordinati. Reticoli e anelli di Boole.
B) BIBLIOGRAFIA
L. DI MARTINO, M.C. TAMBURINI, Appunti di algebra, CLUED, 1990.
I.N. HERSTEIN, Algebra, Editori Riuniti, 1982.
N. JACOBSON, Basic Algebra I, Free & Company, 1989.
C. MARCHIONNA TIBILETTI, V. ZAMBELLI, Esercizi di algebra, Masson, 1987.
F. AYRES, Theory and problems of matrices, Schaum's Series, McGraw-Hill, 1962.
F. AYRES, Theory and problems of Modern Algebra, Schaum's Series, McGraw-Hill, 1962.
C) AVVERTENZE
N.B. - Il Prof. Maria Clara Tamburini riceve gli studenti il lunedì dalle ore 14,30 alle ore 16,30 nel suo studio.
22
2. Algebra superiore (un modulo): prof.
ANDREA LUCCHINI
A) PROGRAMMA DEL CORSO
Introduzione alla teoria dei gruppi: concetti fondamentali ; gruppi liberi e gruppi finitamente presentati; gruppi nilpotenti e localmente nilpotenti; p-gruppi finiti; gruppi risolubili e sottogruppi di Hall; gruppi di permutazione k-transitivi e primitivi; proprietà di finitezza nei gruppi infiniti; metodi computazionali in teoria dei gruppi; il processo di enumerazione di Todd-Coxeter; conseguenze della classificazione dei gruppi semplici e problemi aperti.
B) BIBLIOGRAFIA
D. J. ROBINSON, A Course in Theory of Groups, Springer-Verlag, New York, 1981.
C) AVVERTENZE
N.B. - Il Prof. Andrea Lucchini riceve gli studenti il giovedì dalle ore 15.00 alle ore 16.00 nel suo studio.
23
24
3. Analisi funzionale: prof. ALBERTO G. SETTI
A) PROGRAMMA DEL CORSO
Il corso si articolerà in due moduli semestrali indipendenti.
Primo modulo: Spazi vettoriali localmente convessi e distribuzioni
Spazi vettoriali topologici, prime proprietà. Spazi vettoriali topologici localmente compatti. Seminorme e spazi localmente convessi. Metrizzabilità e normabilità. Spazi di Frechet. Esempi.
Operatori lineari e funzionali lineari continui. Il teorema di Hahn-Banach in spazi localmente convessi e conseguenze. Lo spazio duale e le topologie deboli. La topologia weak* e il teorema di Banach-Alaoglu.
Spazi di funzioni test e distribuzioni. Operazioni sulle distribuzioni. Supporto e supporto singolare di una distribuzione. Struttura locale delle distribuzioni. Distribuzioni a supporto compatto e convoluzione di distribuzioni.
Lo spazio di Schwartz S delle funzioni a decrescenza rapida. Lo spazio S' delle distribuzioni temperate. La trasformata di Fourier su S e su S'. Teoria L2 della trasformata di Fourier.
Spazi di Sobolev. Trasformata di Fourier di distribuzioni a supporto compatto. Teoremi di Paley-Wiener. Esempi di trasformate di Fourier di distribuzioni.
Applicazioni a equazioni differenziali. Operatori ellittici e ipoellittici. Regolarità ellittica. Soluzioni fondamentali e teorema di Malgrange-Ehrernpreis.
Secondo modulo: Algebre di Banach e Teoria Spettrale
Algebre di Banach. Omomorfismi e funzionali lineari moltiplicativi. Elementi invertibili e il teorema di Gelfand-Mazur. Algebre di Banach commutative e relativo spettro. La trasformata di Gelfand. Algebre di Banach semisemplici. Algebre con involuzione e B* algebre. Il teorema di Gelfand-Naimark. Esempi.
La -algebra degli operatori limitati su uno spazio di Hilbert. Sottoalgebre autoaggiunte massimali abeliane. La
-algebra degli operatori limitati su uno spazio di Hilbert. Sottoalgebre autoaggiunte massimali abeliane. La -algebra degli operatori di moltiplicazione su L
-algebra degli operatori di moltiplicazione su L
2 (d ). Il teorema spettrale per sottoalgebre autoaggiunte massimali. Il teorema spettrale per famiglie commutative di operatori normali: forma moltiplicativa. Proiezioni ortogonali e misure a valori di proiezioni. Integrazione di funzioni limitate rispetto a una misura a valori di proiezioni .La risoluzione spettrale di una famiglia commutativa di operatori normali e la seconda forma del teorema spettrale. Il calcolo funzionale. Caratterizzazione spettrale degli operatori compatti e autoaggiunti. Operatori illimitati su uno spazio di Hilbert. Operatori chiusi, simmetrici e autoaggiunti. Criteri di autoaggiuntezza. La trasformata di Cayley. Integrazione di funzioni misurabili rispetto ad una misura a valori di proiezioni. Le due forme del teorema spettrale per operatori autoaggiunti. Il teorema spettrale per un operatore normale. Calcolo funzionale. Applicazioni alle equazioni di evoluzione.
). Il teorema spettrale per sottoalgebre autoaggiunte massimali. Il teorema spettrale per famiglie commutative di operatori normali: forma moltiplicativa. Proiezioni ortogonali e misure a valori di proiezioni. Integrazione di funzioni limitate rispetto a una misura a valori di proiezioni .La risoluzione spettrale di una famiglia commutativa di operatori normali e la seconda forma del teorema spettrale. Il calcolo funzionale. Caratterizzazione spettrale degli operatori compatti e autoaggiunti. Operatori illimitati su uno spazio di Hilbert. Operatori chiusi, simmetrici e autoaggiunti. Criteri di autoaggiuntezza. La trasformata di Cayley. Integrazione di funzioni misurabili rispetto ad una misura a valori di proiezioni. Le due forme del teorema spettrale per operatori autoaggiunti. Il teorema spettrale per un operatore normale. Calcolo funzionale. Applicazioni alle equazioni di evoluzione.
B) BIBLIOGRAFIA
Primo modulo.
W. RUDIN, Functional Analysis, Mc-Graw Hill, capp. 1, 3, 6-8.
Si segnalano inoltre:
K. YOSIDA, Functional Analysis, Springer.
R. LARSEN, Introduction to Functional Analysis, Dekker.
Secondo modulo.
W. RUDIN, Functional Analysis, Mc-Graw Hill, capp. 10-13.
Si segnalano inoltre:
K. YOSIDA, Functional Analysis, Springer.
M. REED, B. SIMON, Methods of Modern Mathematical Physics, volumi 1 e 2, Academic Press.
C) AVVERTENZE
N.B. - Il Prof. Alberto Secchi riceve gli studenti dopo le lezioni nel suo studio.
24
4. Analisi matematica I: prof.
MAURIZIO PAOLINI
A) PROGRAMMA DEL CORSO
Elementi di logica. Proposizioni e connettivi. Predicati e quantificatori.
La teoria degli insiemi di Zermelo-Fraenkel. Costruzione dei numeri reali. Proprietà di Archimede e densità dei numeri razionali. Costruzione dell'insieme dei numeri complessi.
Limiti e continuità per funzioni reali di variabile reale. Massimo e minimo limite. Successioni e sottosuccessioni. Teorema di Bolzano-Weierstrass. Criterio di convergenza di Cauchy. Il teorema di esistenza degli zeri. Inversa di una funzione continua. Il teorema di Weierstrass. Uniforme continuità. Serie a termini reali. Serie a termini reali positivi. Criteri del confronto, della radice, del rapporto e di condensazione. Serie assolutamente convergenti e prodotto secondo Cauchy di due serie. Criterio di Leibniz. Estensioni al caso complesso.
La funzione esponenziale in ambito complesso. Funzioni circolari. Logaritmi ed esponenziali con base arbitraria. Funzioni circolari inverse. Il teorema fondamentale dell'algebra.
La derivata. I teoremi di Rolle, Cauchy e Lagrange. Applicazione allo studio di funzioni. I teoremi di L'Hôpital. La formula di Taylor. Funzioni convesse.
La teoria dell'integrazione secondo Riemann. Integrabilità delle funzioni monotòne e delle funzioni continue. Il teorema fondamentale del calcolo integrale. Formule di integrazione per sostituzione e per parti. Integrazione delle funzioni razionali. Integrali impropri e relazione con le serie. Integrazione a valori complessi.
Equazioni differenziali lineari del primo ordine. Equazioni differenziali lineari del secondo ordine a coefficienti costanti. Equazioni differenziali a variabili separabili.
B) BIBLIOGRAFIA
M. DEGIOVANNI, ANALISI MATEMATICA I, DISPENSE DEL CORSO.
J.P. CECCONI, G. STAMPACCHIA, Analisi matematica I: funzioni di una variabile, Liguori, Napoli, 1974.
C. CITRINI, Analisi matematica I, Boringhieri, Torino, 1991.
G. GILARDI, Analisi Uno, McGraw-Hill, Milano, 1992.
E. GIUSTI, Analisi matematica I, Boringhieri, Torino, 1984.
C.D. PAGANI, S. SALSA, Analisi matematica, vol. I, Masson, Milano, 1990.
G. PRODI, Analisi matematica, Boringhieri, Torino, 1970.
C) AVVERTENZE
N.B. - Il Prof. Maurizio Paolini riceve gli studenti dopo le lezioni nel suo studio.
25
26
5. Analisi matematica II: prof. MARCO DEGIOVANNI
A) PROGRAMMA DEL CORSO
Spazi unitari e spazi normati. Spazi metrici, intorni, aperti e chiusi. Limite e continuità di un'applicazione. Successioni. Spazi metrici completi. Teorema delle contrazioni. Serie. Spazi metrici compatti per successioni e per ricoprimenti. Compattezza negli spazi euclidei. Teorema di Weierstrass. Uniforme continuità. Spazi metrici connessi. Nozioni di equivalenza fra metriche. Spazi normati ed unitari di dimensione finita.
Derivata direzionale e differenziale. Calcolo differenziale in dimensione finita. Derivate direzionali di ordine superiore e loro simmetria. Formula di Taylor. Studio di massimi e minimi locali. I teoremi di inversione locale e delle funzioni implicite. Sottovarietà. Teorema dei moltiplicatori di Lagrange. Forme quadratiche ed autovalori.
La misura di Hausdorff in uno spazio euclideo. Misure esterne in uno spazio euclideo. Funzioni misurabili, funzioni integrabili e funzioni sommabili. Teoremi di passaggio al limite sotto il segno di integrale. Teorema di Fubini. Formula dell'area e teorema di cambiamento di variabile. Integrali dipendenti da un parametro. Formula di Gauss-Green e teorema della divergenza. Teorema di Stokes.
Sistemi di equazioni differenziali ordinarie del primo ordine. Esistenza ed unicità locale per il problema di Cauchy. Soluzioni massimali. Il caso lineare. Wronskiano e metodo di variazione delle costanti. Equazioni differenziali lineari a coefficienti costanti.
Forme differenziali lineari. Integrale lungo una curva. Forme differenziali esatte. Forme differenziali chiuse. Aperti semplicemente connessi. Campi di vettori solenoidali. Potenziale vettore su aperti stellati.
B) BIBLIOGRAFIA
R. A. ADAMS, Calcolo differenziale 2. Funzioni di più variabili, Casa Editrice Ambrosiana, Milano, 1993.
C. CITRINI, Analisi matematica 2, Boringhieri, Torino,1992.
W. H. FLEMING, Functions of several variables, Springer-Verlag, Berlin, 1977.
G. GILARDI, Analisi due, McGraw-Hill Italia, Milano, 1993.
E. GIUSTI, Analisi matematica 2, Boringhieri, Torino, 1984.
C.D. PAGANI, S. SALSA, Analisi matematica, vol. 2, Masson, Milano, 1991.
G. PRODI, Analisi matematica, parte II, Editrice Tecnico Scientifica, Pisa, 1971.
W. RUDIN, Principi di analisi matematica, McGraw-Hill Italia, Milano, 1991.
N.B. - Verranno inoltre distribuite delle dispense sui vari argomenti del corso.
C) AVVERTENZE
N.B. - Il Prof. Marco Degiovanni riceve gli studenti prima delle lezioni nel suo studio.
26
6. Analisi numerica (I modulo): prof.
MAURIZIO PAOLINI
A) PROGRAMMA DEL CORSO
Teoria degli errori: errore assoluto/relativo, condizionamento di problemi matematici, propagazione dell'errore, rappresentazione floating point, stabilità di algoritmi.
Risoluzione numerica dei sistemi lineari: eliminazione di Gauss, strategie pivotali, metodi compatti, fattorizzazione di Choleski, metodi iterativi di Jacobi, Gauss-Seidel, SOR. Metodo del Gradiente coniugato.
Calcolo degli autovalori di una matrice: metodo delle potenze e potenze inverse, trasformazioni di similitudine di Householder e di Givens, fattorizzazione QR e metodo QR.
Calcolo degli zeri di funzioni nonlineari: bisezione, regula falsi, secanti, Newton, ordine di convergenza, iterazione funzionale, accelerazione di Aitken.
B) BIBLIOGRAFIA
V. COMINCIOLI, Analisi numerica, McGraw-Hill, Milano, 1990.
K.E. ATKINSON, An introduction to numerical analysis, J. Wiley & Sons, New York, 1966.
C) AVVERTENZE
N.B. - Il Prof. Maurizio Paolini riceve gli studenti dopo le lezioni nel suo studio.
27
28
7. Analisi numerica (II modulo): prof. FRANCO PASQUARELLI
A) PROGRAMMA DEL CORSO
Approssimazione di funzioni: interpolazione, minimi quadrati, best approximation. Integrazione numerica: formule di Newton-Cotes e di Gauss. Equazioni differenziali: metodi numerici per il problema di Cauchy.
B) BIBLIOGRAFIA
V. COMINCIOLI, Analisi numerica, McGraw-Hill, Milano, 1990.
K.E. ATKINSON, An introduction to numerical analysis, J. Wiley & Sons, New York, 1966.
C) AVVERTENZE
N.B. - Il Prof. Franco Pasquarelli riceve gli studenti dopo le lezioni nel suo studio.
28
8. Analisi superiore: prof.
ROBERTO LUCCHETTI
A) PROGRAMMA DEL CORSO
Il corso si concentra su problemi di ottimizzazione in ambito convesso, specialmente dal punto di vista della buona posizione del problema e della sua stabilità. Si rivolge agli studenti di ogni indirizzo. In particolare può essere utile agli studenti dell'indirizzo applicativo, in quanto si sofferma anche sugli algoritmi per trovare punti di minimo in problemi vincolati, ed in presenza di funzioni anche non derivabili ovunque.
Il corso è articolato in due moduli indipendenti, anche se, per seguire il secondo modulo è assai utile avere almeno le conoscenze di base fornite dal primo modulo. In dettaglio:
Primo Modulo:
Funzione convesse: generalità, funzioni convesse estese, proprietà di continuità, principali operazioni in convessità, il sottodifferenziale convesso, il sottodifferenziale approssimato, teoria della dualità, algoritmi per la minimizzazione di funzioni convesse.
Secondo Modulo:
introduzione alle tipologie ed alle convergenze sullo spazio dei chiusi di uno spazio metrico, topologie classiche e topologie moderne, equivalenze fra le topologie. Applicazione agli epigrafici delle funzioni.
Approfondimento delle topologie di Mosco, bounded-Hausdorff e slice. Continuità di operazioni fondamentali secondo le varie topologie.
Problemi ben posti secondo Tykhonov, Levitin-Polyak e in senso forte.
Stabilità di un problema minimo.
Relazioni fra stabilità e buona posizione.
Prerequisiti per il corso:
Analisi 1 e 2 e qualche elemento di Analisi Funzionale. Se alcuni studenti non conoscessero tali elementi di Analisi Funzionale, durante il corso saranno brevemente richiamati.
B) BIBLIOGRAFIA
Saranno in distribuzione di volta in volta dispense sulle lezioni svolte.
C) AVVERTENZE
N.B. - Il Prof. Roberto Lucchetti riceve gli studenti il venerdì dalle ore 13.00 alle ore 15.00.
29
30
9. Chimica generale ed inorganica: prof. LAURA E. DEPERO
A) PROGRAMMA DEL CORSO
 Concetti di base: Unità di misura, elementi e composti, nomenclatura, stechiometria.
Concetti di base: Unità di misura, elementi e composti, nomenclatura, stechiometria.
 Termodinamica chimica elementare: Richiami sulle proprietà dei gas, primo principio, termochimica, secondo principio, applicazioni.
Termodinamica chimica elementare: Richiami sulle proprietà dei gas, primo principio, termochimica, secondo principio, applicazioni.
 Equilibri di fase: Diagrammi di stato di una sostanza pura, proprietà delle soluzioni, miscele di liquidi volatili, diagramma di stato di due componenti.
Equilibri di fase: Diagrammi di stato di una sostanza pura, proprietà delle soluzioni, miscele di liquidi volatili, diagramma di stato di due componenti.
 Equilibrio chimico: La costante di equilibrio, acidi, basi e sali, equilibri di solubilità, reazioni accoppiate.
Equilibrio chimico: La costante di equilibrio, acidi, basi e sali, equilibri di solubilità, reazioni accoppiate.
 Elettrochimica: Ossido-riduzioni, celle elettrochimiche, celle elettrochimiche commerciali, elettrolisi, applicazioni.
Elettrochimica: Ossido-riduzioni, celle elettrochimiche, celle elettrochimiche commerciali, elettrolisi, applicazioni.
 Legame chimico: Struttura dell'atomo, teoria di Lewis, legame ionico, legame covalente, geometria molecolare, teoria del legame di valenza, orbitali molecolari.
Legame chimico: Struttura dell'atomo, teoria di Lewis, legame ionico, legame covalente, geometria molecolare, teoria del legame di valenza, orbitali molecolari.
 Coesione e struttura: Origine della coesione, struttura dei cristalli, legge di Bragg, l'impacchettamento compatto, strutture meno compatte.
Coesione e struttura: Origine della coesione, struttura dei cristalli, legge di Bragg, l'impacchettamento compatto, strutture meno compatte.
 Cenni di chimica organica e di chimica dell'ambiente.
Cenni di chimica organica e di chimica dell'ambiente.
B) BIBLIOGRAFIA
P. W. ATKINS, Elementi di Chimica Fisica, Zanichelli.
P. W. ATKINS, Chimica Generale, Zanichelli.
B. H. MAHAN, Termodinamica Chimica Elementare, Casa Editrice Ambrosiana.
L. PAULING, General Chemestry, Dover.
P. W. ATKINS, Chimica Fisica, Zanichelli.
C) AVVERTENZE
N.B. - Il Prof. Laura E. Depero riceve gli studenti il lunedì dalle ore 14.00 alle ore 16.00 nel suo studio.
30
10. Esperimentazioni di Fisica I: prof.
LORENZO AVALDI
A) PROGRAMMA DEL CORSO
Parte prima
Introduzione all'analisi degli errori. Lo studio delle incertezze nelle misure fisiche.
Descrizione preliminare dell'analisi degli errori. Errori casuali ed errori sistematici. Come rappresentare ed utilizzare gli errori. Errori relativi. Media e deviazione standard. Deviazione standard come l'incertezza in una singola misura. La deviazione standard della media.
Istogrammi e distribuzioni. Distribuzione normale. Giustificazione della media come la miglior stima. Deviazione standard come il limite di confidenza del 68%. Propagazione degli errori. Livello di confidenza.
Rigetto dei dati: criterio di Chauvenet.
Il problema di combinare misure separate. La media pesata.
Metodo dei minimi quadrati. Covarianza e correlazione.
Il test del 2 per una distribuzione. Definizione generale di
2 per una distribuzione. Definizione generale di 2. Gradi di libertà e
2. Gradi di libertà e 2 ridotto. Probabilità per il
2 ridotto. Probabilità per il 2.
2.
Introduzione alle esperienze di laboratorio.
Parte seconda
8 esperienze di laboratorio: cinematica, dinamica del corpo rigido e termodinamica.
B) BIBLIOGRAFIA
Per la prima parte:
TAYLOR, Introduzione all'analisi degli errori, Zanichelli, Bologna, 1986.
C) AVVERTENZE
N.B. - Il Prof. Lorenzo Avaldi riceve gli studenti il venerdì dalle ore 16.30 alle ore 17.30 nel suo studio o in laboratorio.
31
32
11. Fisica generale I. prof. RODOLFO BONIFACIO
A) PROGRAMMA DEL CORSO
Nozioni introduttive
1. Introduzione
Scopo della fisica e metodo scientifico. Osservazioni oggettive e soggettive. Grandezze fisiche, grandezze fondamentali e derivate. Sistemi di unità di misura. Misura delle lunghezze. Misura dei tempi. Dimensioni ed equazioni dimensionali. Misure relative ed assolute. Errori.
2. Vettori
Grandezze scalari e vettoriali. Vettore e vettore applicato. Algebra vettoriale. Componenti di un vettore. Grandezze vettoriali e loro dimensioni. Grandezze vettoriali applicate in punti. Campi vettoriali. Prodotto scalare tra due vettori (prodotto esterno). Prodotto vettoriale tra due vettori (prodotto interno). Prodotto di tre vettori. Derivata di un vettore. Integrale di un vettore. Definizione di gradiente. L'operatore gradiente.
3. Cinematica
Sistemi di riferimento. Spostamenti. Gradi di libertà. Traiettoria e legge oraria. Equazione del moto. Moto rettilineo uniforme. Velocità. Moto rettilineo vario. Accelerazione. Moto rettilineo uniformemente accelerato. Moto armonico. Moto di un punto con traiettoria in un piano. Moto circolare uniforme. Moto circolare uniforme e moti armonici. Moto di un punto con traiettoria qualsiasi in 3D. Moti centrali. Velocità areolare. Composizione e scomposizione dei moti.
Meccanica newtoniana
4.1 Dinamica del punto materiale.
Legge di inerzia. Terne di riferimento inerziali. Concetto di forza. Concetto di massa inerziale. Secondo principio della dinamica. Quantità di moto ed impulso. Terzo principio della dinamica. Azione e reazione Reazioni vincolari. Misura delle forze. Critica ai concetti di spazio e tempo assoluti. Limiti della meccanica newtoniana. Forze ed interazioni fondamentali.
32
4.2 Gravitazione newtoniana
Introduzione. Leggi di Keplero. Moto dei pianeti e dei satelliti. Legge di gravitazione universale. Forze centripete. Deduzione newtoniana della velocità orbitale minima. g come campo gravitazionale. Simmetria del campo gravitazionale. La forza di gravitazione come forza centrale. Determinazione della costante universale. Massa inerziale e massa gravitazionale. Energia potenziale di gravitazione. Energia meccanica di un sistema gravitazionale. Concetto di forza peso.
4.3 Lavoro e energia del punto materiale.
Definizione di lavoro. Definizione di potenza. Definizione di impulso. Teorema del lavoro e dell'energia cinetica (T). Forze conservative e non conservative. Forze di attrito statico e dinamico e forze viscose come esempi di forze non conservative. Campi di forza conservativi. Energia potenziale (U). Funzione energia potenziale, U (xyz), e relazione F= -gradU. Forze conservative e conservazione dell'energia meccanica. Equilibrio stabile ed instabile. Forze centrali come forze conservative. Moti oscillatori semplici, smorzati e forzati. Pendolo lineare e non lineare.
4.4 Momento angolare (della quantità di moto) e momento di una forza.
Definizione di momento di un vettore. Momento angolare (momento della quantità di moto). Conservazione del momento angolare. Teorema del momento angolare. Teorema del momento dell'impulso. Momento di una forza.
4.5 Sistemi di riferimento inerziali e non inerziali.
Sistemi di riferimento inerziali e deduzione dell'equazione del moto F= ma (esempi).Sistemi di riferimento non inerziali e relatività dei moti. Moto di precessione e formule di Poisson. Concetto di velocità ed accelerazione di trascinamento. Le forze apparenti, centrifuga e di Coriolis. Le forze apparenti in generale. Pendolo di Foucault. Critica einsteniana al concetto di forza apparente. Esempi di sistemi di riferimento inerziali e non inerziali.
4.6 Meccanica dei sistemi di punti.
Definizione di centro di massa e moto del centro di massa. Quantità di moto di un sistema. Teorema della quantità di moto. Principio di conservazione della quantità di moto. Teorema del momento angolare e principio di conservazione del momento angolare. Teorema del lavoro e dell'energia cinetica nei sistemi di punti. Teoremi di Köning. Esempi di moti rototraslatori (energia cinetica di traslazione e rotazione).
4.7 Corpo rigido.
Centro di massa di un continuo rigido. Rotazioni con proprietà di simmetria. Definizione di momento d'inerzia e suo significato meccanico. Calcolo del momento d'inerzia. Teorema degli assi paralleli. Energia rotazionale e traslazionale di un corpo rigido. Equilibrio statico di un corpo rigido.
4.8 Urti
Impulso ed urto. Urti elastici e conservazione della quantità di moto e dell'energia cinetica. Urti non elastici. Urti in 2D e 3D. Urti con un vincolo.
Termodinamica
5.1 Termometria
Concetto di temperatura. Caratteristica termometrica, funzione termometrica, termometro. Misure empiriche della temperatura.
5.2 Calorimetria
Concetto di calore come quantità di energia scambiata. Calori specifici e calorimetri. Calori latenti e propagazione del calore (conduzione, convezione, irraggiamento). Importanza fisica dell'irraggiamento. Cenni al corpo nero e alla radiazione del corpo nero. Cenni alla formula di Planck. Formula di Stefen-Boltzmann.
5.3 Trasformazioni di un sistema termodinamico
Stato di un sistema. Trasformazioni reversibili e irreversibili. Esperienza di Joule. Energia meccanica macroscopica e sua trasformazione. Lavoro e calore. Primo principio della termodinamica. Energia interna come funzione di stato della variabile termodinamica temperatura. Conferme sperimentali del primo principio della termodinamica. Il primo principio come principio di conservazione dell'energia.
5.4 Gas ideali
Definizione di gas ideale. Trasformazioni isoterme, isocore e isobare. Equazione di stato dei gas ideali. Calori specifici e capacità termiche molari. Relazione di Mayer. Significato di calore specifico a pressione costante e a volume costante. Ciclo di Carnot e altri cicli reversibili.
33
34
5.5 II principio della termodinamica
Enunciato di Clausius e di Kelvin-Planck. Equivalenza dei due enunciati. Teorema di Carnot. Macchina frigorifera. Reversibilità e irreversibilità. Temperatura termodinamica assoluta. Teorema di Clausius. La funzione di stato entropia. Trasformazioni reversibili e irreversibili. L'entropia in varie trasformazioni reversibili. Entropia dei sistemi dell'ambiente e dell'universo. Diagrammi T-S. Entropia e processi spontanei.
Teoria cinetica dei gas.
Gas reali
Formula del virale e equazione di van der Waals. Termometro a gas. Boltzmann e il principio del caos molecolare e distribuzione equiprobabile delle velocità. Le basi della fisica statistica. Funzione distribuzione delle velocità e spazio delle velocità. Deduzione microscopica dell'equazione di stato dei gas ideali. Temperatura e energia. Equipartizione dell'energia. Calori specifici e gradi di libertà.
Nota: in grassetto sono riportati i paragrafi di fondamentale importanza. In corsivo sono riportati gli argomenti di carattere più speculativo ai fini del corso.
34
12. Fisica generale II: prof.
FULVIO PARMIGIANI
A) PROGRAMMA DEL CORSO
Analisi vettoriale - Gradiente - Operatore - Divergenza - Rotore - Teoremi fondamentali del gradiente, della divergenza e del rotore - Distribuzione delta di Dirac - Teoria dei campi vettoriali.
- Divergenza - Rotore - Teoremi fondamentali del gradiente, della divergenza e del rotore - Distribuzione delta di Dirac - Teoria dei campi vettoriali.
Elettrostatica: I campi elettrostatici, divergenza e rotore dei campi elettrostatici - Potenziale elettrico - Lavoro ed energia in elettrostatica - Conduttori - Cenni alle tecniche di calcolo dei potenziali - Campi elettrostatici nella materia - Polarizzazione - Spostamento elettrico - Dielettrici lineari - Legge di Lorentz - Legge di Biot-Savart - Divergenze e rotore di B - Potenziale vettore magnetico - Forza elettromotrice - Legge di Faraday - Equazioni di Maxwell - Formulazione potenziale della Elettrodinamica - Energia e momento in Elettrodinamica - Equazioni delle onde elettromagnetiche - Onde elettromagnetiche in mezzi non conduttori - Onde elettromagnetiche in conduttori - Relatività speciale - Meccanica relativistica - Elettrodinamica relativistica (cenni)-
Introduzione all'Ottica fisica - Interferenza - Diffrazione - Riflessione - Rifrazione - Polarizzazione - Radiazioni elettromagnetiche (cenni).
B) BIBLIOGRAFIA
D. J. GRIFFITHS, Introduction to electrodynamics, Prentice Hall, (U.S.A.).
C. MENCUCCINI, V. SILVESTRINI, Fisica II (Elettromagnetismo e Ottica), Liguori.
C) AVVERTENZE
N.B. - Il Prof. Fulvio Parmigiani riceve gli studenti il lunedì dalle ore 9.00 alle ore 12.00 nel suo studio.
35
36
13. Fisica matematica (un modulo): prof. CLAUDIO GIORGI
A) PROGRAMMA DEL CORSO
Il corso si propone di fornire alcune conoscenze sulla conduzione del calore e sui fenomeni di transizione di fase dipendente dalla temperatura. Gli argomenti affrontati saranno i seguenti:
Richiami di termomeccanica dei materiali semplici.
Materiali con memoria termica:
Flusso di calore ed energia interna in conduttori rigidi con memoria termica lineare (modelli Coleman-Gurtin e di Gurtin-Pipkin), restrizioni termodinamiche, condizioni iniziali ed al contorno, equazione del calore di Maxwell-Cattaneo, secondo suono e velocità finita di propagazione del calore.
Transizione di fase dipendente dalla temperatura.
_ Transizione solido-liquido:
fenomeni di fusione e solidificazione (acqua-ghiaccio), modello di Stefan, effetti di rilassamento e modelli di Frémond-Visintin, energia di interfaccia e diffusione di fase, modelli di tipo "phase-field" (Ginzburg-Landau, Cahn-Hillard, Caginalp, Penrose-Fife,  ), generalizzazioni e compatibilità termodinamica, cenni sui modelli anisotropi (dendriti) e irreversibili (uovo sodo).
), generalizzazioni e compatibilità termodinamica, cenni sui modelli anisotropi (dendriti) e irreversibili (uovo sodo).
_ Transizione solido-solido:
fenomeni di transizione austenite-martensite, pseudoelasticità e modelli di Villaggio-Muller, modelli isotropi e anisotropi di Gurtin-Fried.
B) BIBLIOGRAFIA
A. MORRO, T. RUGGERI, Propagazione del calore ed equazioni costitutive, Quaderni del C.N.R.-GNFM, Bologna, 1984.
M BROKATE, J. SPREKELS, Hysteresis and phase transition, Springer, Berlin, 1996
Verranno fornite anche fotocopie di articoli in inglese.
C) AVVERTENZE
Il corso ha la durata di un semestre accademico e prevede solo lezioni teoriche. Deve essere inoltre rispettata la precedenza di "Istituzioni di Fisica Matematica (I Modulo)".
N.B. - Il Prof. Claudio Giorgi riceve gli studenti il venerdì dopo la lezione nel suo studio.
36
14. Fisica superiore: prof.
GIANCARLO CAVALLERI
A) PROGRAMMA DEL CORSO
Storia dell'astronomia dalle origini all'età moderna. Coordinate astronomiche e descrizione geometrica attuale dell'Universo. Cinematica dell'universo: sua espansione. Teorie cosmologiche dall'inizio dell'era moderna fino a circa un trentennio fa. La teoria del "big bang" e la formazione di tutti gli oggetti celesti noti. Teoria dell'evoluzione stellare. L'evoluzione passata e futura dell'universo. Teorie cosmologiche attuali. Utilizzazione metafisica dei risultati cosmologici.
B) BIBLIOGRAFIA
G. CAVALLERI, L'origine e l'evoluzione dell'universo, Tecniche Nuove, Milano 1990.
N.B. - Il Prof. Giancarlo Cavalleri riceve gli studenti dopo le lezioni e gli altri giorni dalle ore 15 alle ore 16 nel suo studio.
37
38
15. Fondamenti dell'informatica: prof. GIOVANNA GAZZANIGA
A) PROGRAMMA DEL CORSO
I modulo
Rappresentazione ed analisi di algoritmi.
Principi di funzionamento di un elaboratore elettronico.
Sintassi e semantica di un linguaggio di programmazione.
Codifica dei dati.
Progetto di programmi con l'utilizzo di un linguaggio di programmazione. Metodologie di programmazione. Questioni relative alla correttezza di algoritmi e programmi.
Elementi di calcolabilità. Autonomi e grammatiche.
II modulo
Problemi di complessità computazionale.
Strutture astratte di dati e loro memorizzazione.
Struttura di un sistema di calcolo. Cenni all'evoluzione delle architetture informatiche e telematiche.
Il software di sistema. Cenno ai sistemi operativi. Analisi del ciclo di vita di un programma. Funzioni di un compilatore.
Confronto tra diversi paradigmi di programmazione.
Cenni alle Basi di Dati.
B) BIBLIOGRAFIA
M. ITALIANI, G. SERAZZI, Elementi di Informatica, ETAS Libri, 1993.
C. BATINI, L. CARLUCCI AIELLO, M. LENZERINI, A. MARCHETTI SPACCAMELA, A. MIOLA, Fondamenti di programmazione dei calcolatori elettronici, Franco Angeli, Milano, 1991.
R. GEOFF DROMEY, Algoritmi fondamentali, Ed, Jackson, Milano, 1990.
D. MANDRIOLI, C. GHEZZI, Theoretical foundations of computer science, John Wiley & Sons, 1987.
B. CODENOTTI, M. LEONCINI, F. ROMANI, Algoritmi e linguaggi, Ed. La Scuola, Brescia, 1990.
G. CIOFFI, V. FALZONE, Manuale di Informatica, III edizione, Calderini, Bologna, 1993.
C) AVVERTENZE
Il corso verrà svolto parte in aula, con lezioni teoriche, e parte in Laboratorio di Informatica, con apposite esercitazioni mirate a fornire una conoscenza operativa degli argomenti trattati in classe.
L'esame del I Modulo consta di una prova scritta e di un'eventuale discussione orale. La prova scritta consiste nella redazione di un programma e nella risoluzione di alcuni esercizi su questioni trattate nel corso.
L'esame del II Modulo consiste in una discussione orale nella quale lo studente dovrà dimostrare la conoscenza degli argomenti in programma e la padronanza degli esercizi svolti e proposti nelle esercitazioni
N.B. - Il Prof. Giovanna Gazzaniga riceve gli studenti dopo le lezioni nel suo studio.
38
16. Fondamenti della matematica (un modulo): prof.
ANTONINO VENTURA
A) PROGRAMMA DEL CORSO
1. La filosofia della matematica nel pensiero antico e medievale
a) La dottrina pitagorica e il matematicismo
b) La conoscenza matematica in Platone e Aristotele
c) L'organizzazione deduttiva del sapere matematico nel sistema di Euclide
d) L'oggetto e il metodo della matematica secondo Tommaso d'Aquino
2. La filosofia della matematica nel pensiero moderno
a) I fondamenti della deduzione in Galileo
b) Il razionalismo matematico di Cartesio
c) La conoscenza matematica in Kant e le
d) forme a priori come fondamento della possibilità della matematica
3. La crisi dell'evidenza matematica e le geometrie non euclidee
4. Il problema dei fondamenti della matematica nel pensiero contemporaneo
a) Il superamento delle concezioni di Cartesio e di Kant e del dogmatismo positivistico
b) Il metodo assiomatico
c) La "crisi dei fondamenti" e il problema della non contradditorietà delle teorie matematiche
d) Costruttivismo, intuizionismo, platonismo. La posizione preicativistica e il concettualismo
e) Il "programma Hilbertiano"
5. I teoremi di incompletezza e il superamento di una concezione puramente formalistica della matematica
a) Il sistema PRA
b) Rappresentazione in PRA della sintassi di una teoria formale e condizioni di derivabilità
c) I teoremi di Gödel
d) Conseguenze dei teoremi di Gödel
39
40
6. Linee essenziali e orientamenti delle ricerche sui fondamenti della matematica nel periodo successivo alla formulazione dei teoremi di Gödel
M. BORGA, D. PALLADINO, Oltre il mito della crisi. Fondamenti e filosofia della matematica nel XX secolo, La Scuola, Brecia, 1997.
E. AGAZZI, D. PALLADINO, Le geometrie non euclidee e i fondamenti della geometria dal punto di vista elementare, La Scola, Brescia, 1998.
S. GALVAN, Introduzione ai Teoremi di Incompletezza, F. Angeli, Milano, 1992.
Ulteriori indicazioni bibliografiche saranno comunicate durante il corso.
C) AVVERTENZE
N.B. - Il Prof. Antonino Ventura riceve gli studenti il giovedì dalle ore 15.00 alle ore 16.00 nel suo studio.
40
17. Geometria 1: prof.
ELENA ZIZIOLI
A) PROGRAMMA DEL CORSO
Algebra lineare: spazi vettoriali su un campo, basi, dimensioni, formula di Grassmann. Omomorfismi fra spazi vettoriali, forme lineari, spazio vettoriale duale. Matrici e determinanti, teorema di Laplace e di Binet, invertibilità di matrici e loro rango. Sistemi lineari, teorema di Cramer e di Rouché-Capelli. Sistemi lineari omogenei. Diagonalizzazione di un endomorfismo: autovalori e autovettori, diagonalizzazione di una matrice quadrata. Forme bilineari e quadratiche, prodotti scalari, spazi vettoriali euclidei. Prodotti hermitiani e spazi unitari: riduzione a forma canonica di una forma quadratica reale.
Spazi affini: Definizione, traslazioni, sottospazi, parallelismo, affinità. Coordinazione di uno spazio affine. Geometria analitica degli spazi affini.
Spazi euclidei: Distanza fra due punti, ortogonalità fra rette, fra piani, fra retta e piano, circonferenze e sfere. Luoghi geometrici fondamentali. Isometrie.
Spazi proiettivi: Definizione, sottospazi proiettivi, coordinate omogenee, rappresentazioni in coordinate omogenee dei sottospazi proiettivi. Cambiamenti di coordinate omogenee e proiettività. Complessificazione.
Curve algebriche reali piane: Ordine, punti semplici e singolari. Coniche, classificazione proiettiva, fasci di coniche, polarità, classificazione affine delle coniche, equazioni canoniche affini, classificazione metrica: assi, fuochi, proprietà focali, equazioni canoniche metriche.
B) BIBLIOGRAFIA
Testi consigliati.
E. S. ERNESI, Geometria I, Bollati Boringhieri, Torino, 1989.
M. STOKA, Corso di geometria, Cedam, Padova, 1987.
R. MORESCO, Esercizi di algebra e di geometria, (V ed), Ed. Libreria Progetto, Padova, 1996.
V. PIPITONE, M. STOKA, Esercizi e problemi di geometria, vol. I, Cedam, Padova.
C) AVVERTENZE
N.B. - Il Prof. Elena Zizioli riceve gli studenti dopo le lezioni nel suo studio.
41
42
18. Geometria II: prof. SILVIA PIANTA
A) PROGRAMMA DEL CORSO
1. Spazi proeittivi su campi
Proprietà del reticolo dei sottospazi, riferimenti proiettivi, coordinate proiettive omogenee e cambiamenti di riferimento; equazioni dei sottospazi; spazi proiettivi e spazi affini. Spazio proiettivo duale, proposizioni grafiche, principio di dualità, teorema di Desargues. Collineazioni di uno spazio proiettivo: omologie, proiettività e loro rappresentazione analitica, teoremi fondamentali, birapporto. Correlazioni, correlazioni proiettive, polarità. Superfici algebriche reali dello spazio proiettivo complesso: ordine, punti semplici e singolari, superfici rigate e di rotazione. Quadriche: classificazione affine, sezioni piane, equazioni canoniche affini. Proprietà metriche.
2. Elementi di topologia generale
Dagli spazi metrici agli spazi topologici: definizione di spazio topologico ed esempi; basi di una topologia. Applicazioni continue e omeomorfismi tra spazi topologici. Sottospazi di uno spazio topologico, prodotto di spazi topologici, spazi quozienti. Assiomi di separazione. Connessione e compattezza. Varietà topologiche.
3. Elementi di geometria differenziale
Varietà differenziabili, spazi tangenti, differenziali, orientabilità; immersioni e sottovarietà, sommersioni; campi vettoriali. Curve differenziali e formule di Frenet; curve regolari di R2 e di R3; curvatura e torsione. Superfici di R3, prima, e seconda forma fondamentale.
B) BIBLIOGRAFIA
G. CASTELNUOVO, Lezioni di geometria analitica, Dante Alighieri, Milano, 1969.
V. CHECCUCCI, A. TOGNOLI, E. VESENTINI, Lezioni di topologia generale, Feltrinelli, Milano, 1972.
E. SERNESI, Geometria 1, Boringhieri, Torino, 1989.
E. SERNESI, Geometria 2, Boringhieri, Torino, 1994.
C) AVVERTENZE
N.B. - Il Prof. Silvia Pianta riceve gli studenti dopo le lezioni nel suo studio.
42
19. Geometria Superiore (I modulo): prof.
MAURO SPERA
A) PROGRAMMA DEL CORSO
Il presente corso si prefigge di fornire un'introduzione elementare e concreta a vari aspetti della moderna geometria differenziale attraverso la discussione di numerosi esempi, che contribuiranno ad approfondire le relazioni con altre branche della matematica, come la topologia algebrica, l'analisi e la fisica matematica.
1. Prologo: geometria differenziale della superficie nello spazio.
Superfici regolari. Prima e seconda forma fondamentale. Teorema di Meusnier. Teorema di Eulero. Curvatura gaussiana. Connessione di Levi Civita e trasporto parallelo. Il Theorema Egregium. Formula di Levi Civita. Geodetiche e loro proprietà intrinseche ed estrinseche. Formula di Gauss per i triangoli geodetici. Teorema di Gauss-Bonnet.
2. Varietà differenziabili.
Definizione e primi esempi. Fibrati vettoriali. Fibrato tangente e cotangente. Campi vettoriali e forme differenziali. Differenziale esterno. Il complesso di de Rham. Gruppi di Lie.
3. Geometria Riemanniana.
Metriche Riemanniane. Connessione di Levi Civita. Tensori di curvatura (Riemann, Ricci, scalare).Geodetiche. Geometrie non euclidee. Il teorema dell'indice di Morse.
4. Geometria simplettica.
Varietà simplettiche. Teorema di Darboux. Orbite coaggiunte, applicazione momento e riduzione simplettica.
5. Varietà Kähleriane.
Varietà hermitiane. La condizione di Kähler e i suoi significati geometrici. Esempi rilevanti.
6. Aspetti topologici.
Omologia e coomologia singolare, coomologia di de Rham. Teorema di de Rham. Teoria di Hodge. Applicazioni: dualità di Poincaré. Teorema di Künneth, topologia delle varietà Kähleriane. Connessioni su fibrati lineari. Curvatura e prima classe di Chern. Il teorema di Weil-Kostant.
43
44
B) BIBLIOGRAFIA
M. DO CARMO, Differential Geometry of Curves and Surfaces, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1976.
M. DO CARMO, Riemannian Geometry, Birkhäuser Basel, Boston, 1992.
D. MCDUFF, D. SALAMON, Introduction to symplectic topology, Clarendon Press, Oxford, 1995.
B. DUBROVIN, A. FOMENKO, S. NOVIKOV, Géométrie Contemporaine, MIR, Moscon, 1982.
S. GOLDBETG, Curvature and Homology, Dover, New York, 1962.
P. GRIFFITHS, J. HARRIS, Principles of Algebraic Geometry, Wiley, New York, 1978.
F. WARNER, Foundations of Differantial Geometry and Lie groups, Scott, Foresman and Co., Glenview, 1971.
44
20. Geometria Superiore (II modulo): prof.
CLAUDIO PERELLI CIPPO
A) PROGRAMMA DEL CORSO
Alcuni punti di Geometria Differenziale, e precisamente:
- Concetti fondamentali del Calcolo Differenziale Assoluto.
- Proprietà differenziali di curve e superfici differenziabili.
- Generalità sugli Spazi Fibrati.
- Sistemi differenziali esterni.
- Teoremi fondamentali della teoria dei Gruppi di Lie.
B) BIBLIOGRAFIA
Appunti dalle lezioni.
Altra bibliografia verrà comunicata durante il corso.
C) AVVERTENZE
N.B. - Il Prof. Claudio Perelli Cippo riceve gli studenti dopo le lezioni nel suo studio.
45
46
21. Intelligenza artificiale: prof. GERMANO RESCONI
A) PROGRAMMA DEL CORSO
Primi concetti di Intelligenza artificiale. La Teoria dei Sistemi come approccio all'intelligenza. Valore Semantico e sintattico. Analisi dei concetti. La Teoria Logica dei Sistemi. Omomorfismi fra Sistemi. Sistemi e Modalità. Sottosistemi. Feed-back. Teoria dei Compartimenti. Reti Neurali. Cenni di Robotica. Logica sfumata. Insiemi Sfumati. Operazioni sugli insiemi sfumati. Teoria dell'evidenza. Introduzione al linguaggio per oggetti. Teoria degli Agents.
B) BIBLIOGRAFIA
E. PESSA, Intelligenza artificiale, Bollati Boringhieri, 1992.
E. PESSA, Reti neurali e processi cognitivi, Di Renzo Editore, Roma, 1993.
T. JACKSON, Neural Computing an introduction, Adam Hilger, 1990.
A. WAYNE WYMORE, Model-Based Systems Engineering, CRC Press, 1993.
G. J. KLIR, B. YUAN, Fuzzy Sets and Fuzzy Logic. Theory and Applications, Prentice Hall, PTR Upper Saddle River, New Jersey 07458, 1995.
J. J. CRAIG, Introduction to Robotics, Addison-Wesley Publishing Company, 1989.
46
22. Introduzione alla teologia dogmatica 1: prof.
SAC. PIERLUIGI PIZZAMIGLIO
A) PROGRAMMA DEL CORSO
1. Il problema e il mistero di Dio.
2. La divina rivelazione.
3. Gesù Cristo e il mistero di Dio.
4. Teologia delle religioni.
B) BIBLIOGRAFIA
1. J. FINKENZELLER, Il problema di Dio, Paoline, 1986 oppure J. IMBACH, Breve corso fondamentale sulla fede, Queriniana, 1993.
2. Lettura e commento della "Dei Verbum" oppure J. SCHARBERT, La Bibbia storia autori messaggi, EDB, 1981.
3. F. ARDUSSO, Gesù Cristo figlio del Dio vivente, San Paolo, 1992.
4. M. DHAVAMONY, Teologia delle religioni, San Paolo, 1997.
C) AVVERTENZE
Il corso prevede un seminario su "Scienze e Fede". Come testo base si userà il volume di A. GANOCZY, Teologia della natura, Queriniana, 1997. Chi frequenta il seminario è esonerato dalla parte 4 del programma.
N.B. - Il Prof. Sac. Pierluigi Pizzamiglio riceve gli studenti dopo le lezioni.
47
48
23. Introduzione alla teologia dogmatica 2: prof. SAC. MAURO ORSATTI
A) PROGRAMMA DEL CORSO
La Chiesa e i sacramenti
Il corso, articolato in due parti, si propone di presentare e di approfondire la realtà storico-teologica della Chiesa e dei sacramenti.
Nella prima parte, più storico-esegetica, si cercherà di illustrare il tema ecclesiale partendo dalle due lettere di Paolo alla comunità di Tessalonica. Si tratta del primo testo scritto della letteratura neotestamentaria e presenta il rapporto vivo tra l'apostolo e una comunità ecclesiale. In generale, tutto il testo dimostra una fine sensibilità ecclesiale.
Nella seconda parte, più teologico-sistematica, il tema sarà presentato seguendo lo schema della costituzione conciliare "Lumen Gentium", con riferimenti alla "Gaudium et Spes", per mostrare origine, valore e finalità della Chiesa. Nel contesto della Chiesa verranno presentati i sacramenti nella loro origine, nel loro sviluppo e nel loro significati.
B) BIBLIOGRAFIA
1. Testi richiesti.
R. FALSINI, L'iniziazione cristiana e i suoi sacramenti, OR, Milano,1992.
M. ORSATTI, 1-2 Tessalonicesi, Queriniana, Brescia, 1996.
S. PIè-NINOT, Introduzione alla ecclesiologia, Piemme, Casale Monferrato, 1994.
"Lumen Gentium" e "Gaudium et Spes" (di questi due documenti del Concilio Vaticano II esistono diverse presentazioni; suggeriamo: L. Sartori, La "Lumen Gentium". Traccia di studio, Messaggero, Padova 1994; G. Campanini (a cura di), "Gaudium et Spes". Introduzione e commento, Piemme, Casale Monferrato, 1986.
2. Testi suggeriti.
IOVINO, La prima lettera ai tessalonicesi, E. D. B., Bologna, 1992.
S. WIEDENHOFER, La Chiesa. Lineamenti fondamentali di ecclesiologia, san Paolo, Cinisello Balsamo, 1994.
C) AVVERTENZE
Al corso verrà affiancato un seminario di studio su: "la comunità ecclesiale nel Vangelo". Bibliografia e tematiche saranno offerte all'inizio del corso.
N.B. - Il Prof. sac. Mauro Orsatti riceve gli studenti dopo le lezioni nel suo studio.
48
24. Introduzione alla teologia morale 3: prof.
RENATO MUSATTI
A) PROGRAMMA DEL CORSO
Morale cristiana e vita nuova in Cristo
1. Un primo momento del corso sarà dedicato a rileggere brevemente la storia della teologia morale, focalizzando un'attenzione forte al momento conciliare. Inoltre, si collocherà lo sguardo al passato e al bisogno di un rinnovamento dentro l'attuale contesto culturale, chiarendo le motivazioni del perchè la morale oggi, sia filosofica che teologica, deve porsi di fronte ai nuovi problemi etici posti dalle trasformazioni culturali scientifiche in atto.
2. Il rinnovamento della teologia morale richiede una rifondazione biblica della morale stessa. Si vedrà come un'etica biblica, nell'AT, è inseparabile dalla questione religiosa: l'Alleanza è il patto nuziale tra Dio e il suo popolo e la torah viene dall'alto ed è sorgente di ogni benedizione. Il NT presenta la centralità di Cristo, il Signore, che con l'annuncio del Regno e delle beatitudini, si propone qui ed ora ai discepoli e chiede che la loro nuova vita si dispieghi nel riconoscerlo e nell'obbedire a Lui come Messia morto e risorto.
Le lettere paoline, soprattutto la lettera ai Galati e ai Romani, chiariscono l'idea di legge; legge non vista in modo sistemico ma "legge di Cristo" in dialogo con la vita e i problemi della comunità.
Ci si soffermerà, inoltre, sulla sintesi di tutta la vita cristiana che Giovanni opera proponendo un rapporto stretto tra il credente in Cristo e la Carità.
3. Struttura dell'etica cristiana.
Dalla persona all'agire come esperienza morale, dalla norma (universalità e determinazione, con particolare attenzione alla "legge naturale") alla coscienza.
4. La risposta negativa all'esigenza morale: il problema della colpa.
5. Possibile cammino di una vita secondo lo Spirito.
B) BIBLIOGRAFIA
H. WEBER, Teologia morale generale, Ed. San Paolo, 1996.
M. CHIODI, Morale fondamentale, Manuale di Base, n. 28, Ed. Piemme, V ed,. 1994.
U. NERI, I fondamenti biblici dell'etica cristiana, EDB, Bologna, 1996.
Una Bibbia, possibilmente la Bibbia di Gerusalemme, ED. Dehoniane, Bologna.
PAPA GIOVANNI PAOLO II, Evangelium vitae, Lettera Enciclica, 25-3-1995.
C) AVVERTENZE
N.B. - Il Prof. Renato Musatti riceve gli studenti prima e dopo le lezioni nel suo studio.
49
50
25. Istituzioni di fisica matematica (I modulo): prof. CLAUDIO GIORGI
A) PROGRAMMA DEL CORSO
Il corso si propone di fornire conoscenze generali sulla termomeccanica dei continui con applicazione ai materiali classici. Gli argomenti affrontati saranno i seguenti:
Richiami ed elementi di algebra ed analisi vettoriale.
Meccanica dei mezzi continui ed equazioni di bilancio:
Cinematica della deformazione, equazioni di bilancio (formulazione globale e locale, lagrangiana e euleriana), equazione di continuità, teorema di Cauchy sugli sforzi interni, teorema della quantità di moto, del momento della quantità di moto e dell'energia cinetica, condizioni iniziali ed al contorno.
Principi della termodinamica ed equazioni costitutive:
Bilancio dell'energia, primo e secondo principio della termodinamica, diseguaglianza di Clausius-Duhem, equazioni costitutive per materiali semplici e principi costitutivi (determinismo, azione locale indifferenza materiale, ecc.), gruppo di simmetria materiale.
Materiali classici:
- Fluidi semplici: fluidi perfetti (barotropici e incomprimibili), fluidi newtoniani e stokesiani (fluidi di Bingham), onde acustiche di piccola ampiezza;
- Solidi termoelastici: teoria dell'elasticità lineare, onde elastiche di piccola ampiezza;
- Solidi viscoelastici: Viscoelasticità lineare;
- Conduttori rigidi: leggi di Fourier e di Cattaneo-Maxwell per il flusso di calore.
Esempi ed esercizi sui materiali classici (fluidi e solidi elastici).
B) BIBLIOGRAFIA
C. BANFI, Introduzione alla Meccanica dei Continui, Cedam, Padova,1990.
M. CIARLETTA, S. IESAN, Elementi di meccanica dei continui con applicazioni, Pitagora, Bologna, 1997.
M. FABRIZIO, La meccanica razionale e i suoi metodi matematici, CAP. 6, (II ED.), Zanichelli, Bologna, 1994
Sulla viscoelasticità e sui conduttori di calore verranno forniti appunti.
C) AVVERTENZE
Il corso ha la durata di un semestre e prevede sia lezioni teoriche, sia lezioni esercitazioni. Inoltre, NON è propedeutico al secondo modulo di "Istituzioni di Fisica Matematica", ma al corso di " Fisica Matematica".
N.B. - Il Prof. Claudio Giorgi riceve gli studenti dopo la lezione di venerdì
50
26. Istituzioni di geometria superiore: prof.
BRUNO BIGOLIN
A) PROGRAMMA DEL CORSO
Funzioni analitiche di una e più variabili complesse e precisamente: funzioni olomorfe; integrale di Cauchy e principio del prolungamento analitico; teorema di Hartogs; lo spazio H ( ) come algebra di Fréchet; teoria della convessità olomorfa e poliedri analitici; teorema di E.E. Levi; singolarità e residui; teorema della rappresentazione conforme.
) come algebra di Fréchet; teoria della convessità olomorfa e poliedri analitici; teorema di E.E. Levi; singolarità e residui; teorema della rappresentazione conforme.
B) BIBLIOGRAFIA
Verrà indicata all'albo durante l'anno accademico.
N.B. - Il Prof. Bruno Bigolin riceve gli studenti dopo le lezioni nel suo studio.
51
52
27. Istituzioni di algebra superiore: prof. MARIA CLARA TAMBURINI
A) PROGRAMMA DEL CORSO
I modulo:
Elementi di teoria di Galois
1. Gruppi di permutazione. Orbite, transitività. Struttura dei gruppi simmetrici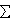
3 e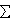 4 . Semplicità dei gruppi alterni di grado > 4. Gruppi risolubili. Teorema di Jordan-Holder.
4 . Semplicità dei gruppi alterni di grado > 4. Gruppi risolubili. Teorema di Jordan-Holder.
2. Campi. Anelli di polinomi a coefficienti in un campo. Radici.
3. Campi di spezzamento e chiusure algebriche. Il teorema fondamentale dell'algebra.
4. Estensioni normali e separabili. Gruppo di Galois di una estensione. Il teorema fondamentale della teoria di Galois.
5. Teorema dell'elemento primitivo. Campi finiti. Polinomi ciclotomici.
6. Criteri per la risolubilità per radicali di una equazione algebrica.
II Modulo:
1. Richiami di algebra lineare: autovalori, forme bilineari, spazi euclidei.
2. Prodotto tensoriale di moduli.
3. Definizione ed esempi di algebre di Lie. Ideali. Omomorfismi.
4. Algebre di Lie nilpotenti e risolubili. Il teorema di Engel.
5. Algebre di Lie semisemplici. Criterio di Cartan e sue conseguenze. Rappresentazioni.
6. Sistemi di radici e gruppo di Weyl. Grafi di Coxeter, diagrammi di Dynkin, matrici di Cartan.
7. Sottoalgebre di Cartan.
8. Cenni ai gruppi semplici di tipo Lie.
B) BIBLIOGRAFIA
Per il I Modulo:
Dispense del docente.
I. KAPLANSKY, Fields and Rings, University of Chicago Press, 1969.
C. PROCESI, Elementi di teoria di Galois, Decibel Editrice, 1982.
Per il II Modulo:
R. W. CARTER, Simple groups of Lie type, J. Wiley and Sons, 1972.
J. HUMPHREYS, Introduction to Lie algebras and representation theory, Springer Verlag, 1972.
N. JACOBSON, Lie algebras, Interscience Publishers, 1962.
N.B. - Il Prof. Maria Clara Tamburini riceve gli studenti dopo l'orario di lezione nel suo studio.
52
28. Istituzioni di analisi superiore: prof.
MARCO DEGIOVANNI
A) PROGRAMMA DEL CORSO
I modulo
Spazi Lp. Completezza. Regolarizzazione per convoluzione e densità delle funzioni regolari. Funzioni continue e periodiche. Densità di polinomi trigonometrici. Esempi di spazi funzionali separabili.
Spazi di Banach. Duale topologico. Forma analitica e forme geometriche del teorema di Hahn-Banach. Il teorema di Banach-Steinhaus. I teoremi dell'applicazione aperta e del grafico chiuso.
Spazi di Hilbert. Proiezione su un convesso chiuso. Caratterizzazione del duale. Il teorema di Lax-Milgram. Sistemi ortogonali completi. Il caso di L2 ( -
-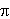 ,
,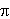
 n).
n).
Operatori limitati in uno spazio di Hilbert. Operatori compatti. La teoria di Riesz-Fredholm. Proprietà spettrali. Decomposizione spettrale per operatori compatti e normali. Cenno al caso degli operatori limitati e normali.
Operatori illimitati in uno spazio di Hilbert. Proprietà spettrali. Decomposizione spettrale per operatori normali con risolvente compatto. Cenno al caso degli operatori illimitati e normali.
II modulo
Spazi di Sobolev. Approssimazione con funzioni regolari. Regole di calcolo. Il teorema di Sobolev. Il teorema di Rellich.
Equazioni ellittiche del secondo ordine in forma di divergenza. Formulazione debole ed alternativa di Fredholm. Teoremi di regolarità.
Il primo modulo è propedeutico al secondo.
B) BIBLIOGRAFIA
I modulo
H. BREZIS, Analisi funzionale - Teoria e applicazioni, Liguori, Napoli, 1986.
M. REED, B. SIMON, Methods of modern mathematical physics. I. Functional analysis, Academic Press, New York-London, 1980.
W. RUDIN, Analisi reale e complessa, Boringhieri, Torino, 1974.
II modulo
H. BREZIS, Analisi funzionale - Teoria e applicazioni, Liguori, Napoli, 1986.
D. GILBARG, N. S. TRUDINGER, Elliptic partial differential equations of second order, Grundlheren der Mathematischen Wissenschaften, 224, Springer-Verlag, Berlin-New York, 1977.
Verranno inoltre distribuite delle dispense sui vari argomenti del corso.
C) AVVERTENZE
N.B. - Il Prof. Marco Degiovanni riceve gli studenti dopo le lezioni nel suo studio.
53
54
29. Istituzioni di fisica matematica (II modulo): prof. CARLO BANFI
A) PROGRAMMA DEL CORSO
1. Prerequisiti di Analisi matematica. Convoluzione; trasformata di Fourier; elementi di teoria delle distribuzioni.
2. Generalità sulle equazioni della Fisica matematica. Classificazione; varietà caratteristiche; problemi ben posti; teorema di Cauchy-Kowalewski; formula di Green.
3. Equazioni del primo ordine. Equazioni quasi lineari; equazioni ai differenziali totali; equazioni non lineari.
4. Operatore di Laplace. Soluzioni fondamentali; formula dei potenziali; teorema del valor medio; principio del massimo; Problemi di Dirichlet e di Neumann¸ funzione di Green; formula di Poisson; soluzioni con metodi funzionali; problema agli autovalori; sviluppo in serie di autofunzioni.
5. Operatore del calore. Soluzioni fondamentali; problema ai valori iniziali; potenziali per l'equazione del calore; problema misto; principio del massimo; teoremi di unicità e di stabilità.
6. Operatore delle onde. Soluzioni fondamentali; problema di Cauchy; formula dei potenziali ritardati; problema misto; teoremi di unicità e stabilità.
B) BIBLIOGRAFIA
G.FOLLAND, Introduction to partial differential equations, Princeton University Press, 1976.
V. S. VLADIMIROV, Equations of Mathematical Physics, M. Dekker, 1971.
W.A.STRAUSS, Partial differential equations, S.Wiley, 1992.
C) AVVERTENZE
N.B. - Il Prof. Carlo Banfi riceve gli studenti il martedì, e il venerdì dalle ore 12.30 alle ore 13.
54
30. Lingua inglese: prof.
ELENA UNGARI
A) PROGRAMMA DEL CORSO
Il corso di Inglese intende offrire una competenza di base tale da permettere l'analisi dei sistemi della lingua in uso. Il programma pertanto si propone quale mezzo di revisione ed approfondimento delle costruzioni grammaticali, sintattiche e lessicali della Lingua Inglese. Agli studenti si richiede quindi una competenza di base nelle quattro abilità linguistiche: leggere, scrivere, ascoltare e parlare.
Gli studenti dovranno dimostrare di conoscere gli argomenti grammaticali contenuti nel libro in adozione, oltre che essere in grado di sostenere una breve conversazione in Lingua Inglese riguardante le tematiche presentate dallo stesso libro di testo.
Si ritiene inoltre indispensabile la lettura, la traduzione e l'analisi di testi matematici raccolti in un'apposita dispensa.
B) BIBLIOGRAFIA
JOHN & LIZ SOARS, Headway elementary, Student's book Workbook, Oxford University Press, 1983 (per principianti).
JOHN & LIZ SOARS, Headway intermediate, Student's book Workbook, Oxford University Press, 1993 (per il livello progredito).
E. UNGARI, English in Mathematics, dispensa acquistabile in sede.
55
56
31. Logica matematica (un modulo): prof. RUGGERO FERRO
A) PROGRAMMA DEL CORSO
1. Elementi di teoria intuitiva degli insiemi. Ordinali e cardinali.
2. Esigenza di un linguaggio formale.
3. La costruzione di un linguaggio formale per descrivere strutture.
4. Verità di una formula in una interpretazione.
5. Validità soddisfacibilità e conseguenza logica. Difficoltà nel controllo.
6. Ricerca di un controllo sintattico della soddisfacibilità.
7. Il metodo degli alberi di confutazione e sua completezza.
8. Cenni ad altri tipi di controlli sintattici e loro completezza.
9. Teoremi di Lowenheim Skolem. Teoremi di compattezza.
10. Isomorfismo, immersione, immersione elementare, elementare equivalenza.
11. Non categoricità delle teorie con modelli infiniti.
12. Non esprimibilità di certe nozioni coinvolgenti l'infinito.
B) BIBLIOGRAFIA
R. FERRO, Appunti per il corso.
T. BELL, M. MACHOVER, A course in mathematical logic, North Holland.
C) AVVERTENZE
N.B. - Il Prof. Ruggero Ferro riceve gli studenti il venerdì dalle ore 18.00 alle ore 19.00 nel suo studio.
56
32. Matematica finanziaria: prof.
FRANCESCO PARIS
A) PROGRAMMA DEL CORSO
I Modulo
1- Capitalizzazione e sconto.
2- Valutazione di rendite certe.
3- Valutazione di rendite aleatorie.
4- Costituzione di capitale e ammortamento di un prestito.
5- Criteri di valutazione degli investimenti.
II Modulo
1- Struttura a termine dei tassi di interesse, duration e convessità.
2- Teoria delle decisioni e scelte di portafoglio.
3- L'equilibrio dei mercati dei capitali.
4- La valutazione degli strumenti derivati.
B) BIBLIOGRAFIA
F. MARELLI, M. D'AMICO, Appunti di matematica finanziaria (Parte prima e seconda), Vannini, Brescia, 1995.
F. PARIS, MAGALì ZUANON, Elementi di finanza matematica, Club, Brescia, 1997.
F. MORICONI, Matematica finanziaria, Il Mulino, Bologna, 1994.
F. CACCIAFESTA, Lezioni di matematica finanziaria classica e moderna, III ed., Giappichelli, Firenze, 1997.
C) AVVERTENZE
N.B. - Il Prof. Francesco Paris riceve gli studenti il giovedì.
57
58
33. Matematiche complementari: prof. MARIO MARCHI
A) PROGRAMMA DEL CORSO
1° modulo
Elementi di geometria euclidea. Il sistema di assiomi di Euclide: il problema del postulato delle parallele. Il sistema di assiomi di Hilbert: le relazioni fondamentali di incidenza, ordinamento e congruenza. La nozione di piano affine: il problema della coordinatizzazione. Dilatazione e traslazioni. La nozione di piano assoluto: i movimenti rigidi; la nozione di perpendicolarità. Il piano euclideo: il teorema di Pitagora.
2° modulo
Elementi di geometria non-euclidea. La configurazione di Saccheri in geometria assoluta. Il paralleleismo iperbolico e le sue proprietà. Immersione del piano iperbolico nel piano proiettivo. Modelli di geometrie non-euclidee iperboliche. Cenni alla geometria non-euclidea ellittica.
Esercitazioni
La teoria della grandezza Numeri naturali, razionali, reali. I problemi classici della geometria elementare. Cenni alla geometria dello spazio: i poliedri.
B) BIBLIOGRAFIA
EUCLIDE, Gli elementi, (a cura di A. Frajese e L. Maccioni), Utet, Torino, 1970.
D. HILBERT, Fondamenti della geometria, Feltrinelli, Milano, 1970.
R. TAUDEA, La rivoluzione euclidea, Bollati Boringhieri, Torino, 1991.
H. KARZEL, K. SöRENSEN, D. WINDELBERG, Einführung in die Geometrie, Vendenhoeck & Ruprecht, Göttingen, 1973.
C) AVVERTENZE
Il primo modulo è propedeutico al secondo.
N.B. - Il Prof. Mario Marchi riceve gli studenti nel suo studio su appuntamento.
58
34. Meccanica razionale: prof.
CARLO BANFI
A) PROGRAMMA DEL CORSO
0. Argomenti propedeutici.
Elementi di algebra lineare. Spazi vettoriali: matrici, trasformazioni lineari, rotazioni; angoli di Eulero; autovettori e autovalori di matrici; spazi affini; prodotto vettoriale.
Elementi di geometria differenziale. Curve regolari; superfici regolari; elementi sulle varietà differenziabili.
1 .Cinematica.
Cinematica del punto. Moto di un punto; traiettoria; legge oraria; velocità; accelerazione; moto in coordinate polari; formula di Binet; velocità in coordinate cilindriche e sferiche.
Cinematica del corpo rigido. Moto del corpo rigido; stato cinetico; teorema di Mozzi.
Moto relativo. Impostazione; relazione tra le velocità; relazione tra le accelerazioni.
Moti rigidi particolari. Moto rigido piano; base e rulletta; moto rigido con un punto fisso.
2. Dinamica.
Punto materiale. Concetti e principi fondamentali; analisi delle forze; equazioni differenziali del moto; punto vincolato; problema statico; momento, potenziale, lavoro; principio delle potenze virtuali; metodo dei moltiplicatori di Lagrange; grandezze cinetiche per il punto materiale; punto soggetto a forze elastiche e di resistenza del mezzo; dinamica del punto vincolato, principio di D'Alembert; integrali primi del moto; teorema dell'energia cinetica; problema di Weierstrass; pendolo semplice; pendolo sferico; dinamica relativa; problema dei due corpi.
Corpo rigido. Sistemi finiti di punti; equazioni cardinali della statica; corpi rigidi; applicazione del principio delle potenze virtuali ai corpi rigidi; statica dei corpi rigidi; sistemi di forze equivalenti; centro di un sistema di forze parallele; baricentro e sue proprietà; casi particolari di corpi rigidi vincolati; grandezze cinetiche per il corpo rigido; momento della quantità di moto di un corpo rigido con un punto fisso; momenti d'inerzia e loro proprietà; momento della quantità di moto in generale; energia cinetica di un corpo rigido; equazioni cardinali della dinamica; integrali primi, teoremi di conservazione; moto di un corpo rigido con asse fisso; moto di un corpo rigido con punto fisso.
3. Elementi di Meccanica analitica.
Sistemi meccanici. Nozione di vincolo; esempi di sistemi vincolati; sistemi olonomi; varietà delle configurazioni.
Movimento, grandezze cinetiche. Movimento di un sistema olonomo; stato cinetico; momento cinetico; energia cinetica.
Meccanica lagrangiana. Potenza, lavoro, potenziale; il problema statico; il principio della minima azione; il sistema lagrangiano; moti per inerzia; generalizzazioni; integrali primi.
Sistemi dinamici. Sistemi dinamici sulle varietà; sistemi di equazioni differenziali; stabilità dell'equilibrio.
Meccanica hamiltoniana. Varietà degli stati; il sistema hamiltoniano; la forma esterna bilineare fondamentale; integrali invarianti; trasformazioni canoniche; parentesi di Poisson; integrali primi.
4. Complementi di Meccanica analitica. Forme differenziali su una varietà; invarianza della 2-forma fondamentale; parentesi di Poisson; trasformazioni canoniche; metodo di Hamilton-Jacobi; integrali primi.
B) BIBLIOGRAFIA
Sulle parti 0, 1, 2 sono disponibili dispense.
Per la parte 3:
C.BANFI, Lezioni di Meccanica analitica, I.S.U. 1997.
C) AVVERTENZE
L'esame è costituito da una prova scritta e da una prova orale. Sono previste anche prove intermedie facoltative.
Ia prova su "Argomenti propedeutici", "Cinematica" e "Dinamica del punto";
IIa prova su " Dinamica del corpo rigido " e Dinamica dei sistemi";
Ogni prova consisterà in due parti:
a) risposte a domande sulla teoria;
b) esercizio.
Alla fine verranno date due valutazioni riassuntive su teoria e su esercizi.
Gli studenti che avranno avuto una valutazione sufficiente negli esercizi saranno esentati dalla prova d'esame scritta.
Gli studenti che avranno avuto una valutazione sufficiente sulla teoria dovranno rispondere nella prova d'esame orale solo su gli "Elementi di Meccanica analitica" e i "Complementi".
N.B. - Il Prof. Carlo Banfi riceve gli studenti il martedì e il venerdì dalle ore 12.30 alle ore 13.
59
60
35. Metodi di approssimazione (un modulo): prof. MAURIZIO PAOLINI
A) PROGRAMMA DEL CORSO
Soluzione di sistemi lineari di grandi dimensioni: approfondimento metodi diretti e metodi iterativi, metodo del gradiente coniugato, precondizionamento, metodi multigrid.
Problemi ai limiti in una dimensione: shooting, differenze finite, elementi finiti.
Problemi ai limiti in più dimensioni: metodo di Galerkin ed elementi finiti, errore di interpolazione, stime di errore nella norma dell'energia.
Equazioni ellittiche (equazione di Poisson): stima di errore in L2.
Equazioni paraboliche (equazione del calore): cenni.
Equazioni iperboliche (equazione delle onde): cenni.
Problemi computazionali: generazione della griglia, assemblaggio delle matrici, ecc.
Metodi adattivi per le equazioni alle derivate parziali.
B) BIBLIOGRAFIA
V. COMINCIOLI, Analisi numerica, Metodi modelli Applicazioni, McGraw-Hill, Milano, 1990.
A. QUARTERONI, A. VALLI, Numerical approximation of partial differential equations, Springer, 1994.
C. JOHNSON, Numerical solution of partial differential equations by the finite element method, Cambridge University Press, Cambridge, 1990.
C) AVVERTENZE
N.B. - Il Prof. Maurizio Paolini riceve gli studenti dopo le lezioni nel suo studio.
60
36. Metodi e modelli per l'organizzazione e la gestione: prof.
LORENZO SCHIAVINA
A) PROGRAMMA DEL CORSO
Il corso è orientato ai modelli classici della R.O. ma con un taglio applicativo svolto mediante le moderne tecniche di programmazione per oggetti (OOP).
I modelli classici verranno svolti durante le ore di esercitazione, che fanno parte integrante del corso.
Durante il primo semestre verranno svolti argomenti di sviluppo di applicazioni in ambiente OOP.
Nel secondo semestre saranno svolti argomenti di teoria e applicazione dei fuzzy sets.
I modelli classici trattati riguardano:
- P.L.
- Scorte
- Code
- PERT
- Modelli stocastici.
B) BIBLIOGRAFIA
HILLIER, LIEBERMAN, Introduzione alla R. O., F. Angeli.
A. GOLDBERG, K. RUBIN, Succeding with objects, Addison-Wesley.
E. GAMMA ET AL., Design Patterns, Addison-Wesley.
M. FOWLER, K. SCOTT, U.M.L. Distilled, Addison-Wesley.
C) AVVERTENZE
Gli argomenti trattati sono riportati nelle dispense del corso.
N.B. - Il Prof. Lorenza Schiavina riceve gli studenti il giovedì dalle ore 10.30 alle ore 12.30 nel suo studio.
61
62
37. Preparazione di esperienze didattiche: prof. GIANFRANCO BERTAZZI
A) PROGRAMMA DEL CORSO
I Modulo:
Elementi della teoria degli errori; misura della densità dei solidi con la bilancia idrostatica; misura della pressione atmosferica con il barometro Fortin; taratura di un barometro aneroide; misura del coefficiente dell'attrito statico; misura dell'umidità relativa, della tensione di vapore e della temperatura del punto di rugiada con lo psicrometro; misura dell'accelerazione di gravità con il pendolo di Borda; misura della tensione superficiale dei liquidi con lo stalagmometro.
II Modulo:
Otto esperienze da scegliere tra le seguenti:
misura dell'intensità luminosa con il fotometro di Bunsen; misura parametri di un telescopio elementare (di Keplero); misura della frequenza di un diapason con il metodo della risonanza; impiego pratico di amperometri e voltmetri; impiego dei condensatori; misura di una resistenza con il ponte di Wheatstone; misura dei coefficienti di induttanza e di mutua induttanza; misura delle extracorrenti di apertura e di chiusura; misura dei parametri di un trasformatore statico; determinazione sperimentale delle caratteristiche di una fotocellula; utilizzazione pratica dell'oscilloscopio e suo impiego per lo studio del caos; costruzione di un radioricevitore elementare a galena.
N.B. - Al termine del II Modulo verrà effettuata una visita didattica presso l'osservatorio astrofisico di Asiago.
B) BIBLIOGRAFIA
Sono disponibili dispense.
C) AVVERTENZE
N.B. - Il Prof. Gianfranco Bertazzi riceve gli studenti subito dopo le lezioni nel suo studio.
62
38. Sistemi di elaborazione dell'informazione: prof.
GIOVANNI SACCHI
A) PROGRAMMA DEL CORSO
I modulo: Generalità sui Sistemi operativi
Concetti fondamentali, classificazione, struttura.
Compiti di un Sistema Operativo:
Gestione dei processi;
Gestione della memoria;
Interfaccia del File system.
Casi di studio:
I Sistemi Unix;
I Sistemi Windows.
Esercitazioni: Introduzione e analisi del linguaggio FORTRAN.
II modulo: Approfondimenti sui Sistemi operativi
Deadlock:
Modellizzazione e caratterizzazione;
Gestione, rilevamento, ripristino.
Processi:
Processi cooperanti;
Thread, esempi;
Processi concorrenti.
Sistemi distribuiti:
Strutture di comunicazione;
Strutture dei sistemi distribuiti;
File System distribuiti.
Casi di studio:
I Sistemi Linux.
Esercitazioni: Approfondimenti del linguaggio FORTRAN e analisi di altri linguaggi ad alto livello.
63
64
B) BIBLIOGRAFIA
A. SILBERSCHATZ, P. GALVIN, Operating Systems concepts, Addison - Wesley, V Ed., 1998.
B. W. KERNIGAN, R. S. PIKE, The Unix programming environment, Prentice Hall, Software Series, 1984.
T. M. R. ELLIS, Programmazione Strutturata FORTRAN 77 (con elementi di FORTRAN 90), Zanichelli, Bologna, II ed., 1997.
C) AVVERTENZE
Modalità d'esame
L'esame del Primo modulo consiste in una prova scritta dedicata alla redazione e alla messa a punto di un programma su uno degli elaboratori del Centro di Calcolo.
L'esame del Secondo modulo consiste in una prova orale in cui lo studente dovrà dimostrare la conoscenza degli argomenti in programma.
N.B. - Il Prof. Giovanni Sacchi riceve gli studenti il mercoledì dalle ore 17 alle ore 18 nel suo studio.
64
39. Sistemi informativi (un modulo): prof.
GIUSEPPE MEREGAGLIA
A) PROGRAMMA DEL CORSO
Obiettivi del corso:
Il corso si propone come ponte tra la cultura aziendale e quella informatica.
Fornisce i concetti, i modelli e le metodologie fondamentali per analizzare l'architettura di un'azienda (contesto, funzioni, comportamenti, prodotti, processi, strategie e fattori critici), per definire il quadro completo delle sue esigenze informative, per progettare criticamente l'architettura generale del sistema informatico e per definire il quadro delle priorità attuative.
Programma delle lezioni:
1-Struttura generale dei sistemi informativi (sistemi, informazione e comunicazione, conoscenza, funzioni informative, processi informativi, sistemi informativi)
2-Sistemi informativi naturali
3-Sistemi informativi artificiali (sistemi artificiali e automazione dei sistemi informativi, strutture tecniche, modelli per l'automazione, sistemi informatici)
4-Rapporti tra sistemi informativi naturali e artificiali
5-Modelli aziendali (modelli aziendali classici, modello di riferimento, processi aziendali)
6-Sistemi informativi aziendali (aspetti informativi nei contesti aziendali, modello generale dei sistemi informativi aziendali, la domanda informativa, i prodotti, la struttura e i modelli analitici del sistema informativo aziendale)
7- Sistemi informativi aziendali automatizzati (SIA) (tecnologie dell'informazione e automazione del SIA, modello generale dei SIA, la domanda informatica, i prodotti del SIA, le strutture del SIA)
8-Tendenze del SIA e del settore IT (i cambiamenti in atto nell'ambiente, la nuova domanda informatica)
9-Strutture e quadro evolutivo delle metodologie per disegnare e dirigere il SIA (teoria dei metodi, quadro delle metodologie informatiche: evoluzione, esigenze, tendenze)
65
66
10-Framework di riferimento: schema generale di BIS-API (impostazione e quadro generale; fasi, sequenze e tempi)
11-Le fasi BIS-API per progettare e dirigere l'innovazione organizzativa e tecnologica (definire l'architettura del sistema azienda, studiare i modelli di direzione e le innovazioni dell'azienda, disegnare l'architettura del SIA, definire il piano e il sistema di direzione del SIA, acquisire, usare e valutare le componenti del SIA)
12-Criteri per dirigere il SIA (quadro di riferimento e ruolo del SIA, compiti delle direzioni, allineamento delle strategie).
B) BIBLIOGRAFIA
M. RICCIARDI, "Architetture aziendali e informatiche", Etas Libri, Milano, 1995.
C) AVVERTENZE
Modalità d'esame:
L'impegno nel lavoro di gruppo, l'edizione di una tesina (professionale anche negli aspetti comunicativi) costituiscono premessa indispensabile per essere ammessi alla prova orale.
66
40. Statistica matematica: prof.
ANGELO ZANELLA
A) PROGRAMMA DEL CORSO
Modulo I: Elementi di Calcolo delle probabilità e di Statistica.
La nozione di probabilità. Presentazione assiomatica della struttura delle probabilità. Vari approcci per assegnare il valore delle probabilità: frequentista, classico, soggettivista, la distribuzione di probabilità condizionata, la formula di Bayes.
Gli spazi probabilistici con supporto euclideo: le variabili aleatorie o casuali. Il caso unidimensionale: la funzione di ripartizione; tipologia delle variabili aleatorie: discrete, assolutamente continue e singolari.
Estensione al caso bidimensionale: variabili marginali e condizionate. Cenni sulle variabili aleatorie multidimensionali.
Descrizione sintetica delle variabili aleatorie: valore medio e momenti; funzioni di regressione nel caso bidimensionale. La disuguaglianza di Chebychev. Famiglie di variabili aleatorie di particolari interesse applicativo (di tipo discreto: ipergeometria, binomiale, di Poisson; di tipo continuo: normale, semplice e doppia).
Le successioni di variabili aleatorie. La funzione caratteristica. Convergenza quasi certa, in probabilità ed in distribuzione. La legge dei grandi numeri; il teorema centrale di convergenza.
Modulo II: Introduzione all'inferenza statistica.
Complementi di calcolo della probabilità. La nozione di informatore statistico e la distribuzione di probabilità condizionata dal valore di un informatore; informatori sufficienti o esaustivi; informatori completi.
Paradigma dell'inferenza parametrica classica. Il campionario casuale: famiglie di variabili casuali ed inferenza campionaria sui parametri delle stesse. Le famiglie esponenziali.
Elementi di teoria della stima statistica di parametri reali. Stimatori, corretti o non distorti, consistenti. Stimatori efficienti. Miglioramento di uno stimatore corretto (teorema di Rao-Blackwell). Condizione di esistenza e reperimento dello stimatore efficiente (Teorema di Lehmann-Scheffé). Limite teorico dell'efficienza: disuguaglianza di Dugué-Rao-Cramèr. L'ottenimento di stimatori consistenti ed asintoticamente efficienti: il criterio della massima verosimiglianza.
Elementi di teoria della verifica statistica delle ipotesi. Nozione di base della teoria delle decisioni in presenza di risultati aleatori: funzione di decisione, rischio, rischio bayesiano. La verifica statistica delle ipotesi come problema di decisione condizionato. Il lemma fondamentale di Neyman-Pearson. Tests uniformemente massimamente potenti.
B) BIBLIOGRAFIA
Per il Modulo I:
G. DALL'AGLIO, Calcolo delle probabilità, Zanichelli, Bologna, 1987.
A. ZANELLA, Argomenti di Statistica metodologica: la struttura del modello probabilistico, Cleup, Padova, 1980.
L. BERTOLI BARSOTTI, Problemi e complementi di calcolo delle probabilità ed inferenza statistica, ISU - Università Cattolica, Milano, 1996.
Testi di cui può essere utile la consultazione:
G. LETTA, Probabilità elementare, Zanichelli, Bologna, 1993.
H. BAUER, Probability theory and elements of measure theory, Accademic Press, London, 1981.
Per il Modulo II:
A. ZANELLA, Appunti delle lezioni di Statistica II: Inferenza Statistica, Univ. Cattolica - Istituto Di Statistica, Milano, 1997.
A.M. MOOD, F.A. GRAYBIL, D.C. BOES, Introduzione alla Statistica, McGraw-Hill Libri, Milano, 1988.
Testi di cui può essere utile la consultazione:
A. AZZALINI, Inferenza statistica: un'introduzione basata sul concetto di verosimiglianza, Springer-Verlag, Berlin, 1992.
E.J. DUDEWICZ, S.N. MISHRA, Modern mathematical statistics, Wiley, New York, 1988.
E.L. LEHMANN,.Theory of point estimation, Wiley, New York, 1985.
E.L. LEHMANN, Testing statistical hypotheses, 2a Ed., Wiley, New York, 1986.
A. RIZZI, Inferenza statistica, UTET Libreria, Torino, 1992.
C) AVVERTENZE
N.B. - Il Prof. Angelo Zanella riceve gli studenti il venerdì dalle ore 15 alle ore 16 nel suo studio.
67
68
41. Storia delle matematiche: prof. ENRICO GAMBA
A) PROGRAMMA DEL CORSO
1° modulo
Le scienze nell'Antichità. I Pitagorici. La matematica come scienza: Euclide, Archimede, Apollonio, Matematica ed astronomia: Ipparco e Tolomeo. Il declino della scienza antica ed i suoi lasciti alla scienza moderna.
La scienza come soggetto storico. Compiti, funzioni, implicazioni etiche, pedagogiche, sociali dell'impresa scientifica nel suo svolgimento storico.
2° modulo
Il calcolo infinitesimale da Cavalieri ad Eulero. Matematica, fisica ed astronomia in Keplero, Galileo,. Newton.
La Rivoluzione scientifica ed il formarsi della coscienza dell'uomo moderno.
B) BIBLIOGRAFIA
1° modulo
P.L. PIZZAMIGLIO, La storia della matematica, ISU.
2° modulo
W. DUNHAM, Viaggio attraverso il genio, Zanichelli.
M. GARGANTINI, Uomo di scienza uomo di fede, Editrice LDC.
N.B. - Per entrambi i moduli saranno anche forniti appunti.
C) AVVERTENZE
I due moduli sono il larga misura indipendenti, pertanto il primo non è propedeutico al secondo.
N.B. - Il Prof. Enrico Gamba riceve gli studenti dopo le lezioni nel suo studio.
68
69
 -algebra degli operatori limitati su uno spazio di Hilbert. Sottoalgebre autoaggiunte massimali abeliane. La
-algebra degli operatori limitati su uno spazio di Hilbert. Sottoalgebre autoaggiunte massimali abeliane. La -algebra degli operatori di moltiplicazione su L
-algebra degli operatori di moltiplicazione su L ). Il teorema spettrale per sottoalgebre autoaggiunte massimali. Il teorema spettrale per famiglie commutative di operatori normali: forma moltiplicativa. Proiezioni ortogonali e misure a valori di proiezioni. Integrazione di funzioni limitate rispetto a una misura a valori di proiezioni .La risoluzione spettrale di una famiglia commutativa di operatori normali e la seconda forma del teorema spettrale. Il calcolo funzionale. Caratterizzazione spettrale degli operatori compatti e autoaggiunti. Operatori illimitati su uno spazio di Hilbert. Operatori chiusi, simmetrici e autoaggiunti. Criteri di autoaggiuntezza. La trasformata di Cayley. Integrazione di funzioni misurabili rispetto ad una misura a valori di proiezioni. Le due forme del teorema spettrale per operatori autoaggiunti. Il teorema spettrale per un operatore normale. Calcolo funzionale. Applicazioni alle equazioni di evoluzione.
). Il teorema spettrale per sottoalgebre autoaggiunte massimali. Il teorema spettrale per famiglie commutative di operatori normali: forma moltiplicativa. Proiezioni ortogonali e misure a valori di proiezioni. Integrazione di funzioni limitate rispetto a una misura a valori di proiezioni .La risoluzione spettrale di una famiglia commutativa di operatori normali e la seconda forma del teorema spettrale. Il calcolo funzionale. Caratterizzazione spettrale degli operatori compatti e autoaggiunti. Operatori illimitati su uno spazio di Hilbert. Operatori chiusi, simmetrici e autoaggiunti. Criteri di autoaggiuntezza. La trasformata di Cayley. Integrazione di funzioni misurabili rispetto ad una misura a valori di proiezioni. Le due forme del teorema spettrale per operatori autoaggiunti. Il teorema spettrale per un operatore normale. Calcolo funzionale. Applicazioni alle equazioni di evoluzione.
 Concetti di base: Unità di misura, elementi e composti, nomenclatura, stechiometria.
Concetti di base: Unità di misura, elementi e composti, nomenclatura, stechiometria. Termodinamica chimica elementare: Richiami sulle proprietà dei gas, primo principio, termochimica, secondo principio, applicazioni.
Termodinamica chimica elementare: Richiami sulle proprietà dei gas, primo principio, termochimica, secondo principio, applicazioni. Equilibri di fase: Diagrammi di stato di una sostanza pura, proprietà delle soluzioni, miscele di liquidi volatili, diagramma di stato di due componenti.
Equilibri di fase: Diagrammi di stato di una sostanza pura, proprietà delle soluzioni, miscele di liquidi volatili, diagramma di stato di due componenti. Equilibrio chimico: La costante di equilibrio, acidi, basi e sali, equilibri di solubilità, reazioni accoppiate.
Equilibrio chimico: La costante di equilibrio, acidi, basi e sali, equilibri di solubilità, reazioni accoppiate. Elettrochimica: Ossido-riduzioni, celle elettrochimiche, celle elettrochimiche commerciali, elettrolisi, applicazioni.
Elettrochimica: Ossido-riduzioni, celle elettrochimiche, celle elettrochimiche commerciali, elettrolisi, applicazioni. Legame chimico: Struttura dell'atomo, teoria di Lewis, legame ionico, legame covalente, geometria molecolare, teoria del legame di valenza, orbitali molecolari.
Legame chimico: Struttura dell'atomo, teoria di Lewis, legame ionico, legame covalente, geometria molecolare, teoria del legame di valenza, orbitali molecolari. Coesione e struttura: Origine della coesione, struttura dei cristalli, legge di Bragg, l'impacchettamento compatto, strutture meno compatte.
Coesione e struttura: Origine della coesione, struttura dei cristalli, legge di Bragg, l'impacchettamento compatto, strutture meno compatte. Cenni di chimica organica e di chimica dell'ambiente.
Cenni di chimica organica e di chimica dell'ambiente.
 2 per una distribuzione. Definizione generale di
2 per una distribuzione. Definizione generale di 2. Gradi di libertà e
2. Gradi di libertà e 2 ridotto. Probabilità per il
2 ridotto. Probabilità per il 2.
2. - Divergenza - Rotore - Teoremi fondamentali del gradiente, della divergenza e del rotore - Distribuzione delta di Dirac - Teoria dei campi vettoriali.
- Divergenza - Rotore - Teoremi fondamentali del gradiente, della divergenza e del rotore - Distribuzione delta di Dirac - Teoria dei campi vettoriali. ), generalizzazioni e compatibilità termodinamica, cenni sui modelli anisotropi (dendriti) e irreversibili (uovo sodo).
), generalizzazioni e compatibilità termodinamica, cenni sui modelli anisotropi (dendriti) e irreversibili (uovo sodo). ) come algebra di Fréchet; teoria della convessità olomorfa e poliedri analitici; teorema di E.E. Levi; singolarità e residui; teorema della rappresentazione conforme.
) come algebra di Fréchet; teoria della convessità olomorfa e poliedri analitici; teorema di E.E. Levi; singolarità e residui; teorema della rappresentazione conforme.
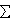
 -
-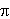 ,
, n).
n).