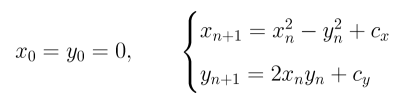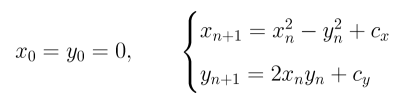L'insieme di Mandelbrot (torna...)
È il luogo dei punti (x,y) del piano che godono
della seguente proprietà: la
successione di punti definita per ricorsione da
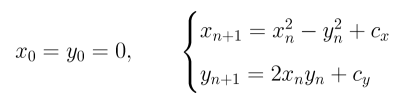
è una successione limitata.
Per chi ha dimestichezza con il piano dei numeri complessi, tale
successione si scrive
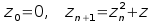 ,
dove
,
dove
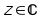 .
Per esempio: per capire
se il punto (2,1) appartiene o no all'insieme di Mandelbrot dobbiamo
costruire la successione
.
Per esempio: per capire
se il punto (2,1) appartiene o no all'insieme di Mandelbrot dobbiamo
costruire la successione
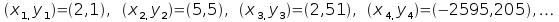 che
è evidentemente illimitata, quindi il
punto (2,1) non appartiene all'insieme di Mandelbrot. Se invece
consideriamo banalmente il punto (-1,0) abbiamo
che
è evidentemente illimitata, quindi il
punto (2,1) non appartiene all'insieme di Mandelbrot. Se invece
consideriamo banalmente il punto (-1,0) abbiamo
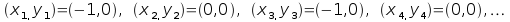 e
la successione continua a oscillare tra i valori (-1,0) e (0,0),
quindi in particolare è limitata. Il punto (-1,0) dunque appartiene
all'insieme di Mandelbrot. Ovviamente i conti non sono sempre così
facili: ad esempio, da una piccola simulazione al calcolatore risulta
che la successione costruita a partire dal punto
(-1.1635189,0.22928247) è limitata e converge verso una successione
periodica di periodo 72!
e
la successione continua a oscillare tra i valori (-1,0) e (0,0),
quindi in particolare è limitata. Il punto (-1,0) dunque appartiene
all'insieme di Mandelbrot. Ovviamente i conti non sono sempre così
facili: ad esempio, da una piccola simulazione al calcolatore risulta
che la successione costruita a partire dal punto
(-1.1635189,0.22928247) è limitata e converge verso una successione
periodica di periodo 72!
Continua...